Solveeit Logo
Login

Question

Question: In the diagram on a lunar eclipse, if the position of sun, earth, moon are shown by \(\left( -4,6 \r...

In the diagram on a lunar eclipse, if the position of sun, earth, moon are shown by (−4,6),(k,−25),(5,−6)\left( -4,6 \right),\left( k,-25 \right),\left( 5,-6 \right) respectively then find the value of k.

Explanation

Solution

Hint: Here, first we should know that in a lunar eclipse, all the three that are sun, earth and moon come in straight line. So, using this logic we have to identify that all the three given points are collinear. After this we use the determinant formula equating it with zero. i.e. 12∣x1−x2x2−x3 y1−y2y2−y3 ∣=0\dfrac{1}{2}\left| \begin{matrix} {{x}_{1}}-{{x}_{2}} & {{x}_{2}}-{{x}_{3}} \\\ {{y}_{1}}-{{y}_{2}} & {{y}_{2}}-{{y}_{3}} \\\ \end{matrix} \right|=0 which is also used to find the area of the triangle when points are lying on vertices.
So, using this formula, we will get the value of K.

Complete step-by-step answer:
Here, we are given three coordinate points i.e. (x1,y1),(x2,y2),(x3,y3)\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right) which is (−4,6),(k,−25),(5,−6)\left( -4,6 \right),\left( k,-25 \right),\left( 5,-6 \right) .
We also know that in lunar eclipse, earth comes between sun and mood. So, all the three i.e. sun, earth and moon come in straight line. So, here we can consider that all the three points are in a straight line which is known as collinear points.
So, here we can use the coordinates (x1,y1),(x2,y2),(x3,y3)\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\left( {{x}_{3}},{{y}_{3}} \right) as the vertices of triangle and find the area of it equating it with zero. Using the formula
12∣x1−x2x2−x3 y1−y2y2−y3 ∣=0\dfrac{1}{2}\left| \begin{matrix} {{x}_{1}}-{{x}_{2}} & {{x}_{2}}-{{x}_{3}} \\\ {{y}_{1}}-{{y}_{2}} & {{y}_{2}}-{{y}_{3}} \\\ \end{matrix} \right|=0
So, substituting the values in the above formula, we get as:
12∣−4−kk−5 6−(−25)−25−(−6) ∣=0\dfrac{1}{2}\left| \begin{matrix} -4-k & k-5 \\\ 6-\left( -25 \right) & -25-\left( -6 \right) \\\ \end{matrix} \right|=0
⇒12∣−4−kk−5 6+25−25+6 ∣=0\Rightarrow \dfrac{1}{2}\left| \begin{matrix} -4-k & k-5 \\\ 6+25 & -25+6 \\\ \end{matrix} \right|=0
Now, multiplying the determinant we get,
⇒12((−4−k)(−19)−31(k−5))=0\Rightarrow \dfrac{1}{2}\left( \left( -4-k \right)\left( -19 \right)-31\left( k-5 \right) \right)=0
⇒12(76+19k−31k+155)=0\Rightarrow \dfrac{1}{2}\left( 76+19k-31k+155 \right)=0
On further simplification, we get
⇒12(231−12k)=0\Rightarrow \dfrac{1}{2}\left( 231-12k \right)=0
On multiplying both sided by 2 we get,
⇒231−12k=0\Rightarrow 231-12k=0
Taking constant on one side and variable on other side, we get
⇒231=12k⇒k=23112=19.25\Rightarrow 231=12k\Rightarrow k=\dfrac{231}{12}=19.25
Graph representation is shown below.

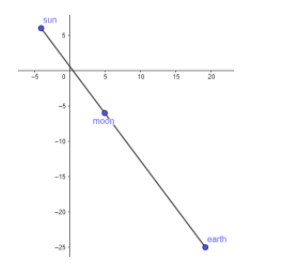
All are in a straight line.
Thus, the value of k will be 19.25.

Note: Another approach for solving this problem is using the slope method for coordinate points (−4,6),(k,−25),(5,−6)\left( -4,6 \right),\left( k,-25 \right),\left( 5,-6 \right) . So, we will use the formula as slope=y2−y1x2−x1slope=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} or slope=y1−y2x1−x2slope=\dfrac{{{y}_{1}}-{{y}_{2}}}{{{x}_{1}}-{{x}_{2}}} . Here, we have three points so, using this formula we get as
slope=y1−y2x1−x2=y2−y3x2−x3slope=\dfrac{{{y}_{1}}-{{y}_{2}}}{{{x}_{1}}-{{x}_{2}}}=\dfrac{{{y}_{2}}-{{y}_{3}}}{{{x}_{2}}-{{x}_{3}}}
On further solving, we get
=6+25−4−k=−25+6k−5=\dfrac{6+25}{-4-k}=\dfrac{-25+6}{k-5}
=31(k−5)=(−19)(−4−k)=31\left( k-5 \right)=\left( -19 \right)\left( -4-k \right)
=31k−155=76+19k=31k-155=76+19k
Thus, on solving we get 12k=231⇒k=23112=19.2512k=231\Rightarrow k=\dfrac{231}{12}=19.25 .
So, using this method we get the same answer.