Question

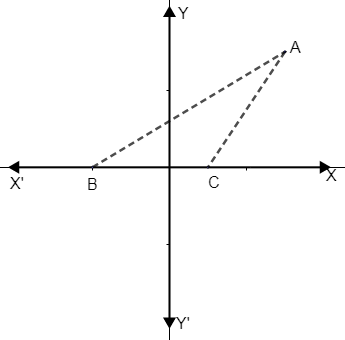
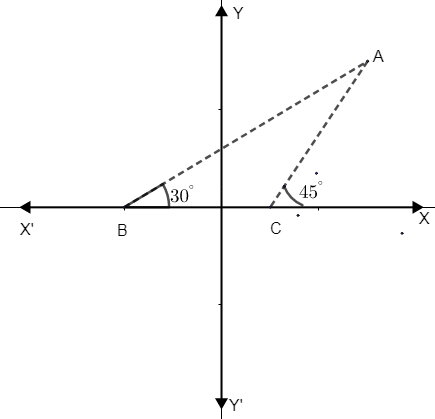
In the diagram given, the equation of AB is $x=\sqrt{3}y+1=0$ and the equation of AC is $x-y-2=0$.
(i) Write down the angles that the line AC and AB make with the positive direction of x – axis.
(ii) Find $\angle BAC$.

Answer 1

Hint: Find the slope of line AB and AC by comparing with $y=mx+b$, which is the formula to find the slope of line. Thus $m=\tan \theta$ and find ${{\theta }_{1}}$ and ${{\theta }_{2}}$ which makes angle with AB and AC. Thus in $\Delta ABC$ apply angle sum property and find $\angle BAC$.

Complete step-by-step answer:
We have been given the line AB, $x=\sqrt{3}y+1$.
Now let us find the slope of line AB.
We know that the slope of the line is given by the formula, $y=mx+b$.
Now given to us the equation, $x=\sqrt{3}y+1$.
Now let us rearrange this equation,

$x=\sqrt{3}y+1$

& \therefore \sqrt{3}y=x-1 \\\ & y=\dfrac{x-1}{\sqrt{3}}=\dfrac{x}{\sqrt{3}}-\dfrac{1}{\sqrt{3}} \\\ \end{aligned}$$ $$\therefore y=\dfrac{x}{\sqrt{3}}-\dfrac{1}{\sqrt{3}}$$, now this is of the form $$y=mx+b$$. Let us compare them. In the equation, slope of a line is given by m. Thus by comparing both equations, we get, $$m=\dfrac{1}{\sqrt{3}}$$. Let us consider $$\theta $$ as the angle which the line AB makes with the positive x – axis. $$\therefore \tan {{\theta }_{1}}=\dfrac{1}{\sqrt{3}}\Rightarrow {{\theta }_{1}}={{\tan }^{-1}}\dfrac{1}{\sqrt{3}}$$ From the trigonometric table we know that, $$\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$$. Thus the value of $${{\theta }_{1}}={{30}^{\circ }}$$. Similarly, we have been given the equation of line of AC as $$x-y-2=0$$. We need to find the slope of AC. $$x-y-2=0$$ $$y=x-2$$, now this is of the form $$y=mx+b$$. By comparing we get m = 1. Thus slope of AC = 1. Hence, $$\tan {{\theta }_{2}}=1$$. $${{\theta }_{2}}={{\tan }^{-1}}1={{45}^{\circ }}$$ From the trigonometric table we know that, $$\tan {{45}^{\circ }}=1$$. Thus, $${{\theta }_{2}}={{45}^{\circ }}$$. Hence, we got the angles that the lines AB and AC make with the positive direction of x – axis. (i) $${{\theta }_{1}}={{30}^{\circ }}$$, angle that line AB makes with the positive direction of x – axis. Similarly, $${{\theta }_{1}}={{45}^{\circ }}$$, angle that line AC makes with the positive direction of x –axis. (ii) Let us now consider the figure, $${{\theta }_{1}}=\angle ABC={{30}^{\circ }}$$. Similarly, $${{\theta }_{2}}={{45}^{\circ }}$$. Now to get, $$\angle ACB=180-45={{135}^{\circ }}$$. We know that straight line angle is $${{180}^{\circ }}$$. Thus to get $$\angle ACB$$, subtract $${{45}^{\circ }}$$ from $${{180}^{\circ }}$$. Let us consider the $$\Delta ABC$$, by angle sum property we know that the sum of all angles in a triangle is $${{180}^{\circ }}$$. Hence, we can say that, $$\angle ABC+\angle ACB+\angle BAC={{180}^{\circ }}$$ We need to find the $$\angle BAC$$. $$\angle ABC={{30}^{\circ }}$$, $$\angle ACB={{135}^{\circ }}$$. Thus, $${{30}^{\circ }}+{{135}^{\circ }}+\angle BAC={{180}^{\circ }}$$. i.e. $$\angle BAC={{180}^{\circ }}-{{30}^{\circ }}-{{135}^{\circ }}$$ $$\begin{aligned} & ={{180}^{\circ }}-{{165}^{\circ }} \\\ & ={{15}^{\circ }} \\\ \end{aligned}$$ Hence we got, $$\angle BAC$$ as $${{15}^{\circ }}$$. Note: The angle inclination of a line is the angle formed by the intersection of the line and the x – axis. Using horizontal run of 1 and m for slope, the angle of inclination, $$\theta ={{\tan }^{-1}}m$$. That’s why we took $$\tan \theta =m$$ here.