Question

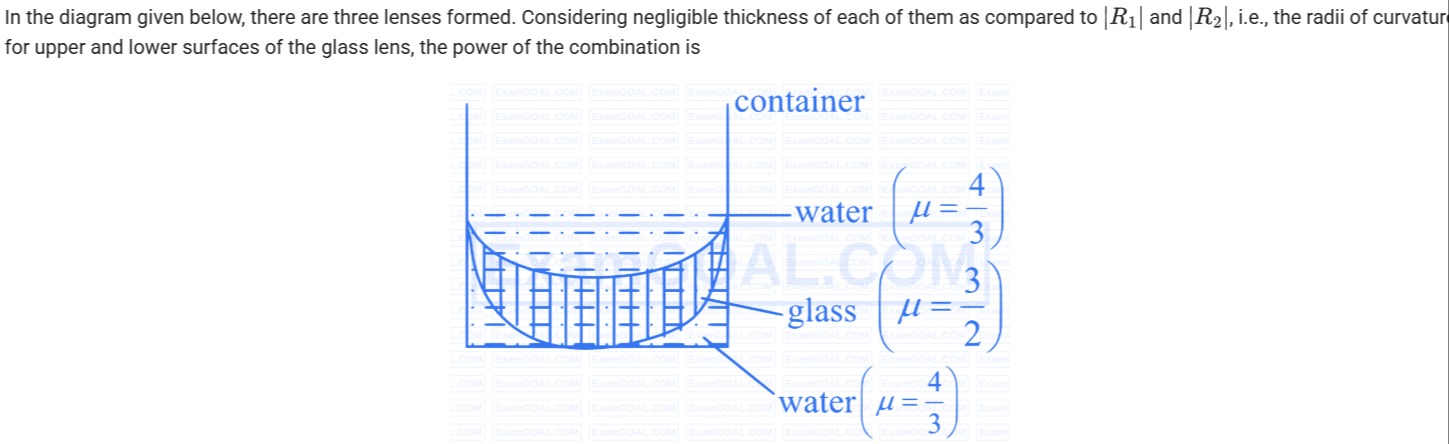
In the diagram given below, there are three lenses formed. Considering negligible thickness of each of them as compared to $|R_1|$ and $|R_2|$, i.e., the radii of curvature for upper and lower surfaces of the glass lens, the power of the combination is

container -water $\mu = \frac{4}{3}$ glass $\mu = \frac{3}{2}$ water $\mu = \frac{4}{3}$

Answer 1

$\Phi=\frac{1}{8}\left(\frac{1}{R_1}-\frac{1}{R_2}\right)$

Answer 2

A thin lens immersed in a medium of refractive index $n_m$ has its effective power given by the lens‐maker’s formula:

$$\frac{1}{f}=\Bigl(\frac{n_{\ell}}{n_m}-1\Bigr)\Bigl(\frac{1}{R_1}-\frac{1}{R_2}\Bigr)$$

where

• $n_{\ell}$ is the refractive index of the lens,
• $n_m$ is the refractive index of the surrounding medium,
• $R_1$ and $R_2$ are the radii of curvature of the two surfaces.

In this problem the glass lens has $n_{\ell}=\tfrac{3}{2}$ and it is immersed in water having $n_m=\tfrac{4}{3}$.

Thus,

$$\frac{n_{\ell}}{n_m}=\frac{3/2}{4/3}=\frac{9}{8}.$$

So the effective power is

$$\Phi=\frac{1}{f}=\Bigl(\frac{9}{8}-1\Bigr)\Bigl(\frac{1}{R_1}-\frac{1}{R_2}\Bigr) =\frac{1}{8}\Bigl(\frac{1}{R_1}-\frac{1}{R_2}\Bigr).$$

For a thin lens in a medium, use $\Phi=(n_{\ell}/n_m-1)(1/R_1-1/R_2)$. Substitute $n_{\ell}=3/2$ and $n_m=4/3$ to get $\Phi=\frac{1}{8}(1/R_1-1/R_2)$.