Question
Question: In the device shown in the figure, the block of mass \(20kg\) is displaced down slightly and release...
In the device shown in the figure, the block of mass 20kg is displaced down slightly and released, it starts oscillating. Pulleys are smooth and massless. Strings and springs are also massless. Find the time period of oscillation (K1=4N/m,K2=4N/m)?
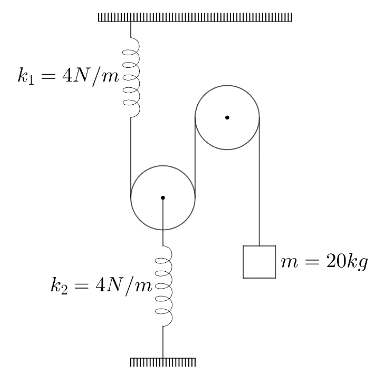
Solution
Before solving this question one should know that simple harmonic motion is only observed when acceleration is proportional to displacement with degree one. In SHM, we can replace acceleration with equation ω2xwhich will help us in finding the time period of the motion of the object.
Formula used:
Tension T=Kx(equal to spring force) and ω=2πf.
Complete step by step answer:
Let’s consider the elongation in spring with spring constant K1 asx1 and K2 as x2 when the mass is being displaced by x units.Now, since the string is the same, displacement of mass will be equal to the net displacement of string. Spring elongation in K1 will be equal to the elongation in the string attached to it. But here comes a problem: the string is rolled over the pulley so the displacement in the string will be divided equally which is x/2.
Talking about the spring with constant K2 since we have assumed its elongation to be x2 the elongation in the string directly attached to it will also be the same, and because of spring with constant K1the pulley attached to that string will create a displacement of x1/2which have to be equal to x2 because of string property. Since the whole system is in equilibrium, we can equate the tension as well.
From the above discussion we get the following result: x2=x1/2
The above relation will be helpful in finding net displacement in terms of string elongation of strings attached to springs and rolled over pulleys.
Now let’s equate the tension to get another relation 2K1x1=K2x2putting the values of spring constant as provided in question we will get
2x1=x2
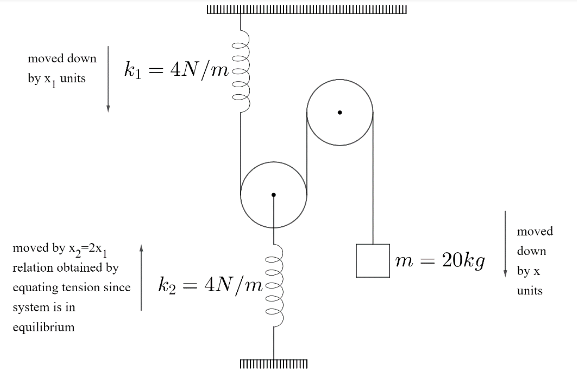
Now let’s write total displacement
x=x1+2x2
Putting the value of x2 as obtained in the relation we will get
x=5x1
Now restoring force, occurring on the mass will be K1x1=ma where a is the acceleration by definition of SHM we can replace acceleration with ω2x (see the hint).
K1x1=mω2(5x1)
On solving and putting the value of spring constant ω=1/5
We know ω=2πf where f is frequency and relation between frequency and time period is f=1/T. On solving we will get T=10π seconds as the answer.
Hence, the time period of oscillation is 10π.
Note: Such a question should be done by visualizing the situation since that will help you in understanding the concept of the spring system. Try to equate the tension and find the net displacement, use both to reach your desired answer.
