Question
Question: In the circular table cover of 32cm, a design is formed, leaving an equilateral triangle ABC in the ...
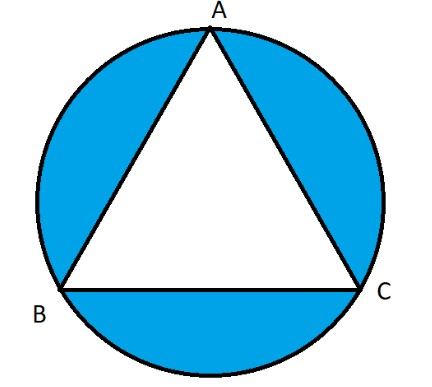
In the circular table cover of 32cm, a design is formed, leaving an equilateral triangle ABC in the middle, as shown in the figure below. Find the area of the design (Shaded region).

[a] (716148−2183)cm2
[b] (719221−5273)cm2
[c] (76288−6723)cm2
[d] None of these
Solution
Hint: Observe that the shaded region is the region of the circle excluding the triangular portion. Hence the area of the shaded region will be equal to the equilateral triangle subtracted from the area of the circle. From the centre of the circle (say O) draw a line (OD) perpendicular to BC and Join OB. Use the fact that the angle subtended by a chord at the centre is twice the angle subtended in the alternate segment to determine ∠BOD. In the triangle BOD, use trigonometry to determine BD and hence determine the length of the side BC. Use the fact that the area of an equilateral triangle of side length a is 43a2. Hence determine the area of the equilateral triangle and hence the area of the shaded region.
Complete step-by-step answer:
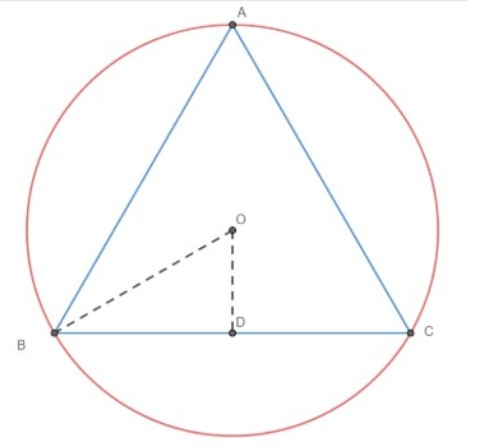
Construction: Draw OD perpendicular BC and join OB.
Now, since ∠BAC is the angle in the alternate segment, we have ∠BOC=2∠BAC
Since OD is the angle bisector of ∠BOC, we have ∠BOD=21∠BOC=21(2∠BAC)=∠BAC.
Since the measure of an angle of an equilateral triangle is 60∘, we have
∠BOD=∠BAC=60∘
Now, we have in triangle OBD,
BD is the side opposite to O and OB is the hypotenuse
Hence, we have
sin(60∘)=OBBD
Now, we have sin60∘=23 and OB=r=32
Hence, we have
32BD=23⇒BD=163
Now, we have BC = 2BD =323
Now, we know that the area of an equilateral triangle of side a is given by A=43a2
Hence, we have
ar(ΔABC)=43(323)2=7683
Also the area of the circle =πr2=722×322=722528
Observe that the shaded region is the region of the circle excluding the triangular portion. Hence the area of the shaded region will be equal to the equilateral triangle subtracted from the area of the circle.
Hence the area of the shaded region =722528−7683
Hence option [d] is correct.
Note: [1] In these types of questions, we need to identify which areas can be calculated from standard formulae. Then we need to think about how the required area can be found using the calculated areas. Like in the above case, the area of the shaded region cannot be calculated directly from standard formulae, but once we observe that this area is the difference of the area of the circle and the triangle, we easily calculate the area of the region.
