Question

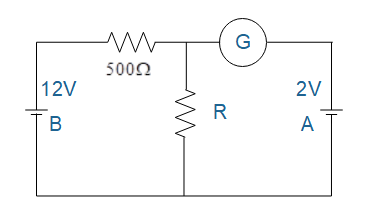
In the circuit, the galvanometer $G$ shows zero deflection. If the batteries $A$and $B$ have negligible internal resistance, the value of resistor$R$ will be

& \text{A}\text{. 1000}\omega \\\ & \text{B}\text{. }500\omega \\\ & \text{C}\text{. 100}\omega \\\ & \text{D}\text{. 200}\omega \\\ \end{aligned}$$

Answer 1

Hint: This question can be solved by using Kirchhoff’s voltage law. Galvanometer shows no deflection, meaning no current will flow through the galvanometer. Consider current only in the first loop. Apply $KVL$then solve. $KVL$can simply be defined as the sum of voltage in a circuit loop.

Complete step by step answer:
The circuit given above has unknown resistance $R$which we need to find out.
A galvanometer is attached between points$D\text{ and E}$. It showed no deflection for current. This means no current flows through the galvanometer.
Let $I$be the current through loop$CDEFHC$.
Apply Kirchhoff’s voltage law in loop$CDHC$,
$-12+500I+2=\dfrac{10}{500}=\dfrac{1}{50}$
$I=\dfrac{1}{50}A$
Since no current flows through galvanometer, same current will flow through branch $DH$
Again apply Kirchhoff’s voltage law,
$\begin{aligned} & -12+500I+RI=0 \\\ & I\left( 500+R \right)=12 \\\ & \dfrac{1}{50}\left( 500+R \right)=12 \\\ & 500+R=600 \\\ & R=600-500 \\\ & R=100\Omega \\\ \end{aligned}$
The value of the resistor$R$will be$100\Omega$
Addition information:

Kirchhoff’s laws are generally used to analyse the electrical circuit that is to calculate the current and resistance in the network. Kirchhoff's law Voltage law and current law are derived on the basis of principle of conservation of energy. Kirchhoff’s law is of two type:
Kirchhoff’s Current Law(KCL)
Statement: The algebraic sum of current entering and leaving at any junction in a circuit is zero.
$i.e.\sum\limits_{{}}^{{}}{i=0}$
Consider a surface as containing the conductor meeting at a point P as shown in figure (a). Now, taking the current flowing away from the junction as positive and current flowing towards the junction as negative, then

{{I}_{1}}-{{I}_{2}}+{{I}_{3}}-{{I}_{4}}+{{I}_{5}}=0 \\\ {{I}_{1}}+{{I}_{3}}={{I}_{2}}+{{I}_{4}}-{{I}_{5}} \\\ \end{array}$$ Kirchhoff’s Current Law(KVL) Statement: The sum of voltage of sources and all potential drop (IR drop) in any closed loop of a network is zero. While applying KVL, positive value of current is taken when we are travelling in the direction of current and e.m.f is taken negative when we travel from negative to positive electrode of source. In ABDA loop, ${{I}_{1}}{{R}_{1}}+{{I}_{2}}{{R}_{2}}+{{I}_{3}}{{R}_{3}}=E$ In ABCA loop, $\begin{aligned} & {{I}_{2}}{{R}_{2}}-{{I}_{5}}{{R}_{5}}-{{I}_{4}}{{R}_{4}}=0 \\\ & {{I}_{2}}{{R}_{2}}={{I}_{5}}{{R}_{5}}-{{I}_{4}}{{R}_{4}} \\\ \end{aligned}$ Answer - (C) Note: In this question we have used Kirchhoff’s voltage law i.e. KCL. One can also use Kirchhoff’s current law. By using KCL also, you will get the same answer. For that you need to just slip current $I$ $DH\text{ and EF}$ and then solve. In this type of question, you cannot use ohm’s law. Using only ohm's law will not give the correct result. Do not get confused between ohm's law and Kirchhoff’ law. Kirchhoff’s laws are used to determine currents and potential difference in the complicated circuit. Ohms law is valid only for graphs passing through origin. KCL is also known as conservation of charge and KVL is known as conservation of energy.