Question
Question: In the circuit shown, when \(R\) is removed an additional resistance of \(72\,\) ohm must be introdu...
In the circuit shown, when R is removed an additional resistance of 72 ohm must be introduced in series with the battery in order to keep the current through 30 ohm resistance unaltered. Hence R is
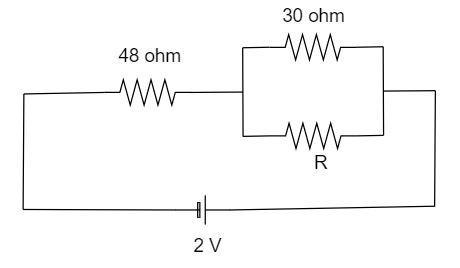
Solution
Hint From the given circuit diagram, calculate the current, potential difference and the total current across each branch. Apply the formula below and substitute the calculated values to find the resistance of the resistor that is removed from the circuit.
Useful formula
The formula of the ohm’s law is given by
V=IR
Where V is the potential difference, I is the current flowing through the circuit and R is the resistance.
Complete step by step solution
It is given that the
Resistor R is removed from the circuit.
The additional resistor that must be connected to main the current, 72Ω
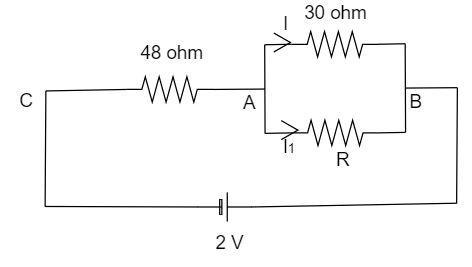
The value of the resistor, R′=30Ω
current =28+30+722=751A
Voltage across CA= Total voltage - voltage across AB
VCA=2−52=58V
Total current =5×488=301A
Since the resistor is connected in parallel, the potential difference developed across each resistor will be the same. Hence
V=V′
By substituting the ohms law in the above step,
I′R=I(30)
Rearranging the obtained equation, we get
I′=R30I
Substituting the value of the resistance in the above equation, we get
I′=75R30=5R2
It is known that in a parallel circuit, the total current flows in the circuit will be equal to the sum of the currents flows in the individual branch.
I=I+I′
Substituting the values of the current in it,
301=751+5R2
By simplify g the above equation by performing carious basic arithmetic operations,
5R2=501
By further simplification of the above equation
R=20Ω
Hence the value of the resistance is obtained as 20Ω .
Note
Remember that in a parallel circuit, the current flowing through the circuit will be the sum of the current flowing through each resistor and the voltage developed across each resistor will be the same. Hence the voltage across one resistor must be the subtraction of the other voltage with the total.
