Question

In the circuit shown the variable resistor $X$ is adjusted so that high resistance voltmeter $V$ shows a reading of $1V$. The resistance then

A) $1.5\Omega$
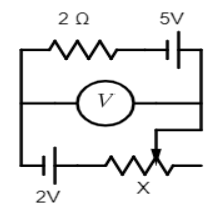
B) $5.0\Omega$
C) $3.0\Omega$
D) $2.5\Omega$

Answer 1

We all know that the sum of all voltages around any closed loop in a circuit must equal zero. We can apply this logic to solve this particular problem.

Complete step by step solution:
Kirchhoff's voltage law (2nd Law) states that the sum of all voltages around any closed loop in a circuit must equal zero.
Let us consider a closed loop in an electric circuit which there are three voltages say ${V_1}$, ${V_2}$, ${V_3}$ around the closed-loop then according to Kirchhoff's voltage law ${V_1} + {V_2} + {V_3} = 0$
Given the circuit diagram:

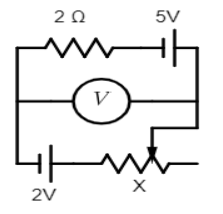
Suppose $i$current is flowing through the circuit and we consider two sides of voltmeter $V$ is $A$ and $B$, so the potential difference will be ${V_A} - {V_B}$.
The modified circuit will be as follow:

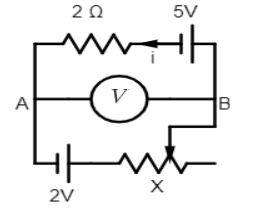
For the upper loop, according to Kirchhoff's voltage law
Through $5V$,
${V_A} + (2\Omega \times i) - 5 - {V_B} = 0$
Let us now rearrange the terms by bringing the voltage terms in left hand side, we get
$\Rightarrow {V_A} - {V_B} = 5 - (2\Omega \times i)$
$\Rightarrow {V_A} - {V_B} = 5 - 2i$
Given, ${V_A} - {V_B} = 1$
Since the voltage terms are equal to one we get,
$5 - 2i = 1$
$\Rightarrow 2i = 4$
$\therefore i = 2$
Hence the current in the circuit is $2A$.
For the lower loop, according to Kirchhoff's voltage law
Through $2V$,
${V_A} + 2 - (X\Omega \times i) - {V_B} = 0$
$\Rightarrow {V_A} - {V_B} = (X\Omega \times i) - 2$
$\Rightarrow {V_A} - {V_B} = Xi - 2$
Given, ${V_A} - {V_B} = 1$and we get current $i = 2A$ .
$(X \times 2) - 2 = 1$
$\Rightarrow 2X = 1 + 2$
$\Rightarrow 2X = 3$
$\therefore X = 1.5$

Hence the value of variable resistance $X$ is $1.5\Omega$. So, option (A) is the correct answer.

Additional information:
The direction of the current and the polarity of the voltage can be assumed as per user. To determine the actual direction and polarity, the sign of the values must be considered.
For example, a current labeled in the clockwise direction with a negative value is flowing anticlockwise.

Note:
The law of Kirchhoff is generally known as the law of Conservation of Energy, as moving around a closed loop in a circuit if we back to the same point from which started there is no work done as well as no voltage loss in this loop we can say. Hence any voltage drops around the loop of the circuit must be equal to any voltage sources met along the way.