Question

In the circuit shown, the resistance $r$ is a variable resistance. If for $r = fR$, the heat generation in $r$ is maximum then the value of $f$ is:

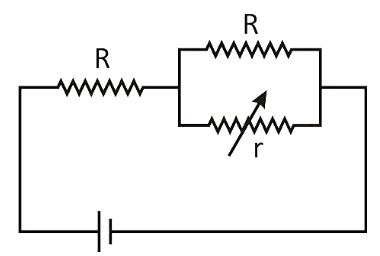
A. $1$
B. $\dfrac{1}{4}$
C. $\dfrac{1}{2}$
D. $\dfrac{3}{4}$

Answer 1

Here we have to use the concepts of series parallel and equivalent resistance. First we have to find the equivalent resistance of the resistors then equate it with the variable resistance to get the value of $f$. The cumulative resistance of the series circuit is equal to the number of the individual resistances. The voltage applied to the series circuit is proportional to the sum of the voltage drops. The voltage drop over the resistor in a series circuit is directly proportional to the size of the resistor.

Complete step by step answer:
The equivalent resistance of a network is the one resistor that could replace the whole network in such a manner that we get the same current with a given applied voltage as we did for a network.First we have to find the equivalent resistance of the given resistors.

Since, the resistances are connected in parallel so, equivalent resistance will be:
${R_{eq}} = \dfrac{R}{2}$
Also, the heat generation is maximum when $r = \dfrac{R}{2}$ i.e. equivalent resistance.
Given,
$r = fR \\\ \Rightarrow \dfrac{R}{2} = fR \\\ \therefore f = \dfrac{1}{2} \\\$
Hence, option C is the correct answer.

Note: Here we have to see whether the resistances are connected in parallel or series. If we mistakenly find the series equivalent resistance then the answer would be wrong. In a series circuit, the output current of the first resistor flows through the input of the second resistor, thus the current in each resistor is same.In a parallel circuit, the entirety of the resistor leads on one side of the resistors are associated together and all the leads on the opposite side are associated together.