Question

In the circuit shown, the power factor of the box is given by $0.5$ and power factor of circuit is given by $\dfrac{{\sqrt 3 }}{2}$. Current leading the voltage. The effective resistance of the box is made by using several resistances. Find the value of resistance of the box.

A. $2{\rm{ }}\Omega$
B. $3{\rm{ }}\Omega$
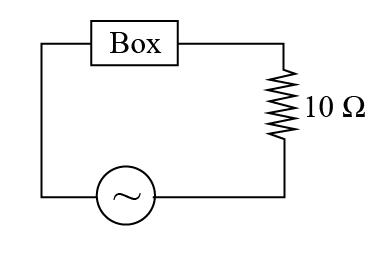
C. $4{\rm{ }}\Omega$
D. $5{\rm{ }}\Omega$

Answer 1

The expression of the power factor of the given circuit is the ratio of effective resistance of the resistor and impedance of the circuit. The impedance of the given L-R circuit is the effect of resistance and reactance of the given circuit as a combine. Mathematically, the impedance of an L-R circuit is equal to the square root of the summation of the square of resistance and reactance of the inductor individually.

Complete step by step answer:
Given:
The power factor of the box is ${P_1} = 0.5$.
The power factor of the circuit is ${P_2} = \dfrac{{\sqrt 3 }}{2}$.
The resistance of the resistor is $R' = 10{\rm{ }}\Omega$.
Let us assume the resistance of the box is R, and we have to find the value of R.

The expression for the power factor of the box is given by:
${P_1} = \dfrac{R}{Z}$……(1)
Here, Z is the impedance of the given circuit.

We know that the expression for impedance of the given box is:
$Z = \sqrt {{R^2} + {X_L}^2}$
Here ${X_L}$ is the reactance of inductor.

Substitute $0.5$ for ${P_1}$ and $\sqrt {{R^2} + {X_L}^2}$ for Z in equation (1).

0.5 = \dfrac{R}{{\sqrt {{R^2} + {X_L}^2} }}\\\ {X_L}^2 = 3{R^2} \end{array}$$ We know that the effective resistance of the given circuit is the summation of resistance R and R’. The expression for the power factor of the circuit is given by: $${P_2} = \dfrac{{R + R'}}{Z}$$……(2) We know that the expression for impedance of the given box is: $$Z = \sqrt {{{\left( {R + R'} \right)}^2} + {X_L}^2} $$ Substitute $$\dfrac{{\sqrt 3 }}{2}$$ for $${P_2}$$ and $$\sqrt {{R^2} + {X_L}^2} $$for Z in the above expression. $$\dfrac{{\sqrt 3 }}{2} = \dfrac{{R + R'}}{{\sqrt {{{\left( {R + R'} \right)}^2} + {X_L}^2} }}$$ Substitute $$3{R^2}$$ for $${X_L}^2$$ and $$10{\rm{ }}\Omega $$ for R’ in the above expression. $$\dfrac{{\sqrt 3 }}{2} = \dfrac{{R + 10{\rm{ }}\Omega }}{{\sqrt {{{\left( {R + 10{\rm{ }}\Omega } \right)}^2} + 3{R^2}} }}$$ On squaring both sides, we get: $$\begin{array}{l} {\left[ {\dfrac{{\sqrt 3 }}{2}} \right]^2} = {\left[ {\dfrac{{R + 10{\rm{ }}\Omega }}{{\sqrt {{{\left( {R + 10{\rm{ }}\Omega } \right)}^2} + 3{R^2}} }}} \right]^2}\\\ {\left( {R + 10{\rm{ }}\Omega } \right)^2} = 9{R^2} \end{array}$$ On solving the above quadratic equation, we will get two distinct values of resistance R. $$R = 5{\rm{ }}\Omega $$, or $$R = \dfrac{{ - 5}}{2}{\rm{ }}\Omega $$ We know that the value of resistance cannot be negative. Therefore, the effective resistance of the given box is $$5{\rm{ }}\Omega $$. **So, the correct answer is “Option D”.** **Note:** While writing the expression impedance of the given circuit do not forget to take the effective resistance of the box and $$10{\rm{ }}\Omega $$. Also, we have to note that the resistance of a resistor cannot have a negative value, so do not get confused in that.