Question
Question: In the circuit shown, the potential difference between A and B is:...
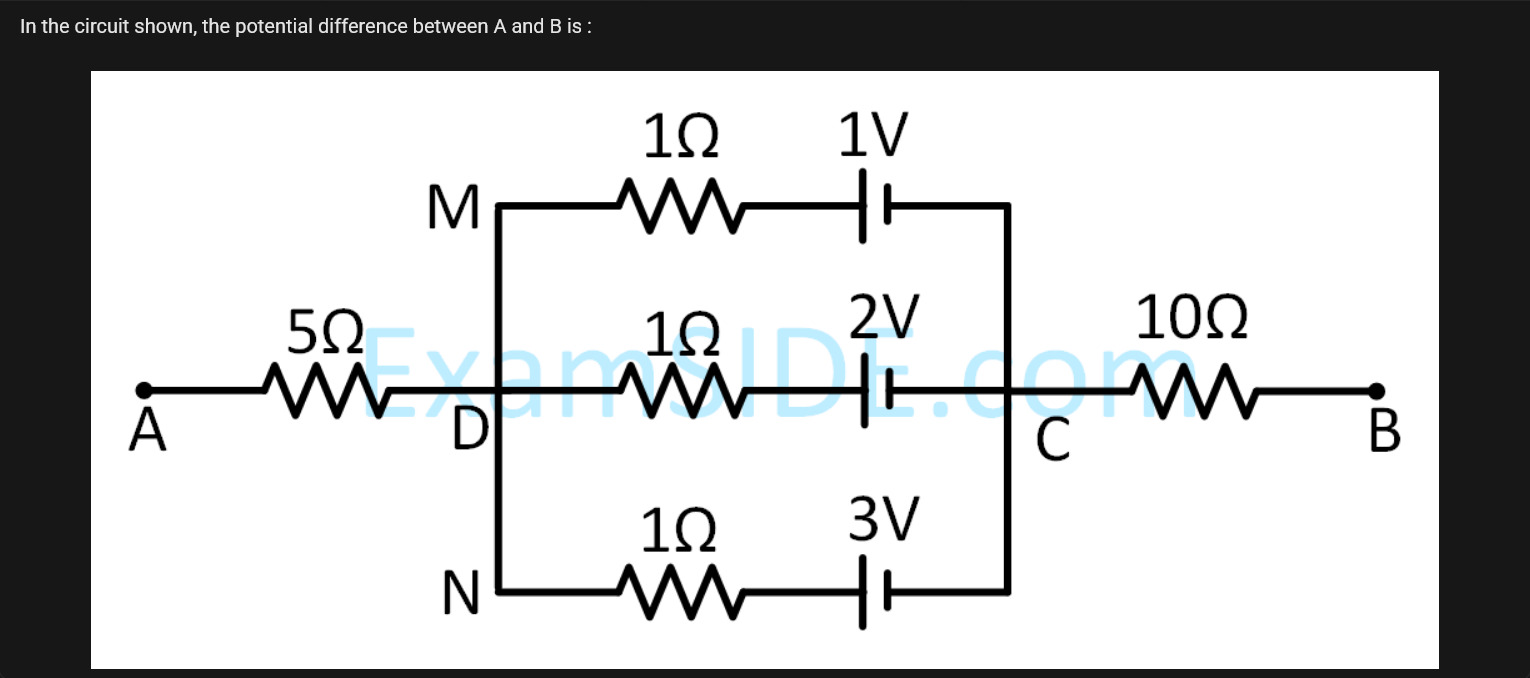
In the circuit shown, the potential difference between A and B is:
92V
46V
30V
0V
92V
Solution
The parallel combination of resistors and voltage sources between nodes D and C can be simplified using Millman's theorem. The equivalent resistance is Req=1Ω1+1Ω1+1Ω11=31Ω. The equivalent voltage source is Eeq=1Ω1+1Ω1+1Ω11Ω1V+1Ω2V+1Ω3V=36V=2V, directed from D to C.
The circuit then becomes a series combination of a 5Ω resistor, the equivalent 2V source and 31Ω resistor (both from D to C), and a 10Ω resistor. The total resistance is Rtotal=5Ω+31Ω+10Ω=346Ω.
Let I be the current flowing from A to B. The potential difference VA−VB can be expressed as the sum of voltage drops and rises in the loop: VA−VB=(VA−VD)+(VD−VC)+(VC−VB) VA−VB=I×5Ω+Eeq+I×10Ω VA−VB=15I+2V.
Alternatively, VA−VB=I×Rtotal=I×346Ω.
Equating the two expressions for VA−VB: 15I+2=346I 2=(346−15)I=(346−45)I=31I I=6A.
Substituting I back into the equation VA−VB=346I: VA−VB=346×6=46×2=92V.
