Question

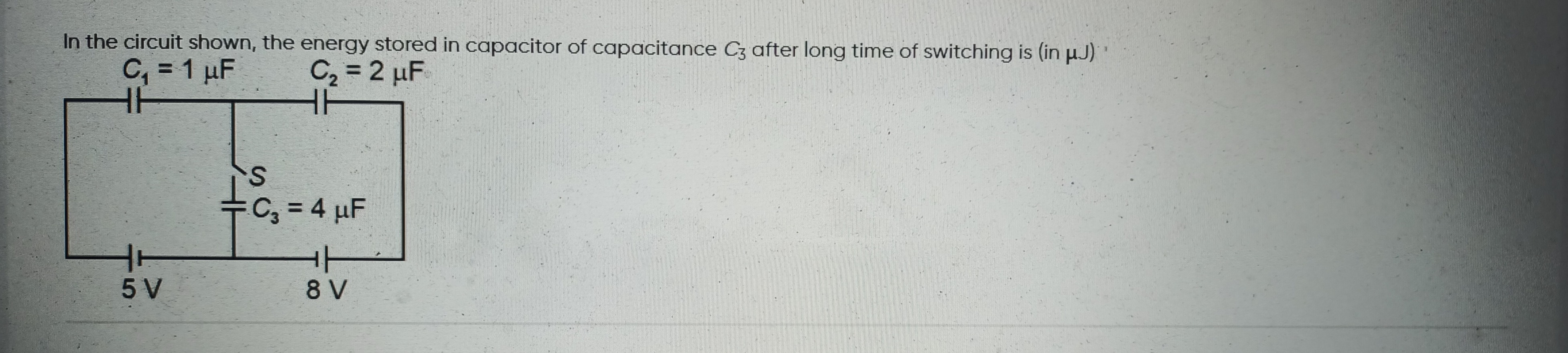
In the circuit shown, the energy stored in capacitor of capacitance $C_3$ after long time of switching is (in $\mu J$). $C_1 = 1 \mu F$ $C_2 = 2 \mu F$

S $C_3 = 4 \mu F$

5 V 8 V

Answer 1

18

Answer 2

To determine the energy stored in capacitor $C_3$ after a long time of switching, we first need to find the potential difference across it. "After a long time of switching" implies that the circuit has reached a steady state. In a DC steady state, capacitors act as open circuits, meaning no current flows through them. However, they are charged and maintain a potential difference across their plates.

Let's label the nodes and their potentials:

1. Let the common bottom wire be the ground, so its potential is $0V$.
2. The 5V battery is connected such that the node below $C_1$ is at $5V$ with respect to ground.
3. The 8V battery is connected such that the node below $C_2$ is at $8V$ with respect to ground.
4. Let the potential of the top common wire (connecting $C_1$, $C_2$, and through switch S, $C_3$) be $V_X$.
5. The switch 'S' is closed after a long time, connecting $C_3$ to the top common wire. The bottom plate of $C_3$ is connected to the ground (0V).

Now, we can apply Kirchhoff's Current Law (KCL) or charge conservation at the top common node. Since no current flows in the steady state, the net charge on the isolated top node must be zero. The charges on the plates connected to this node are $Q_1$, $Q_2$, and $Q_3$.

The charge on a capacitor plate is given by $Q = C \Delta V$, where $\Delta V$ is the potential difference across the capacitor, measured from the plate in question to the other plate.

For $C_1$: The potential difference across $C_1$ is $(V_X - 5V)$. So, $Q_1 = C_1(V_X - 5)$.

For $C_2$: The potential difference across $C_2$ is $(V_X - 8V)$. So, $Q_2 = C_2(V_X - 8)$.

For $C_3$: The potential difference across $C_3$ is $(V_X - 0V) = V_X$. So, $Q_3 = C_3(V_X)$.

According to charge conservation at the top node: $Q_1 + Q_2 + Q_3 = 0$ $C_1(V_X - 5) + C_2(V_X - 8) + C_3(V_X) = 0$

Substitute the given values: $C_1 = 1 \mu F$, $C_2 = 2 \mu F$, $C_3 = 4 \mu F$. $1(V_X - 5) + 2(V_X - 8) + 4(V_X) = 0$ $V_X - 5 + 2V_X - 16 + 4V_X = 0$

Combine terms with $V_X$: $(1 + 2 + 4)V_X - (5 + 16) = 0$ $7V_X - 21 = 0$ $7V_X = 21$ $V_X = \frac{21}{7} = 3V$

So, the potential of the top common node is $3V$. The potential difference across capacitor $C_3$ is $V_{C3} = V_X - 0V = 3V$.

Now, calculate the energy stored in capacitor $C_3$ using the formula $U = \frac{1}{2} C V^2$: $U_3 = \frac{1}{2} C_3 V_{C3}^2$ Given $C_3 = 4 \mu F = 4 \times 10^{-6} F$ and $V_{C3} = 3V$. $U_3 = \frac{1}{2} (4 \times 10^{-6} F) (3V)^2$ $U_3 = \frac{1}{2} (4 \times 10^{-6}) (9)$ $U_3 = 2 \times 9 \times 10^{-6} J$ $U_3 = 18 \times 10^{-6} J$ $U_3 = 18 \mu J$

The energy stored in capacitor $C_3$ is $18 \mu J$.