Question

In the circuit shown, the current in the $1\Omega$ resistor is

A. 1.3A, from P to Q
B. 0A
C. 0.13A, from Q to P
D. 0.13A, from P to Q

Answer 1

As a very first step, you could assume directions for current in every arm in the given circuit. Then you could consider two loops as per your convenience. After that, you could apply kirchoff’s current law each of these loops. Then by doing necessary substitutions find the answer.

Complete answer:
In the question, we are given a circuit and we are supposed to find the current across the $1\Omega$ resistor. Let us assume current direction for all the arms of the circuit.

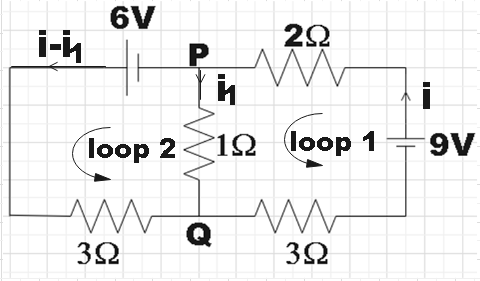
Now, we could apply kirchhoff's voltage law in either of the loops that are marked in the above figure.
For loop 1, on applying kirchhoff's voltage law we get,
$+9-2i-{{i}_{1}}-3i=0$
$\Rightarrow 9={{i}_{1}}+5i$ ………………………………………… (1)
Now, for loop 2, on applying kirchhoff's voltage law, we get,
$+6-\left( i-{{i}_{1}} \right)3+{{i}_{1}}=0$
$\Rightarrow 3i=6+4{{i}_{{{1}_{{}}}}}$
$\Rightarrow i=\dfrac{6+4{{i}_{1}}}{3}$ ………………………………………. (2)
Now, we could simply substitute (2) in equation (1) and thus get,
${{i}_{1}}+5\left( \dfrac{6+4i}{3} \right)=9$
$\Rightarrow 3{{i}_{1}}+30+20{{i}_{1}}=27$
$\Rightarrow 23{{i}_{1}}=-3$
$\therefore {{i}_{1}}=-0.13A$
Therefore, we found that the current across the $1\Omega$ resistor is 0.13A and the negative sign indicates that the direction of the current is opposite to that we assumed that is from Q to P is the correct direction of current.

Hence, option C is found to be the correct answer.

Note:
While solving this question, we found how significant is the role played by signs. You must take care while assigning signs as per known convention while applying kirchoff’s law. Also, it is not necessary that the assumed direction for current in the first step is always right. Following the rest of the steps by assigning the correct sign will give you the answer correctly.