Question

In the circuit shown the cells A and B have negligible resistances. For ${V}_{A}=12V$, ${R}_{1}=500\Omega$ and R=100$\Omega$ the galvanometer (G) shows no deflection. The value of ${V}_{B}$ is:-
A). 12V
B). 6V
C). 4V
D). 2V

Answer 1

To calculate the voltage ${V}_{B}$, you should know the value for resistance and current. Resistance is given so we have to find the current first. So, find the value of current in a loop having ${V}_{A}$ using the formula for current across two series resistors. Then, using the obtained current and given resistance find voltage ${V}_{B}$.

Complete step-by-step solution:

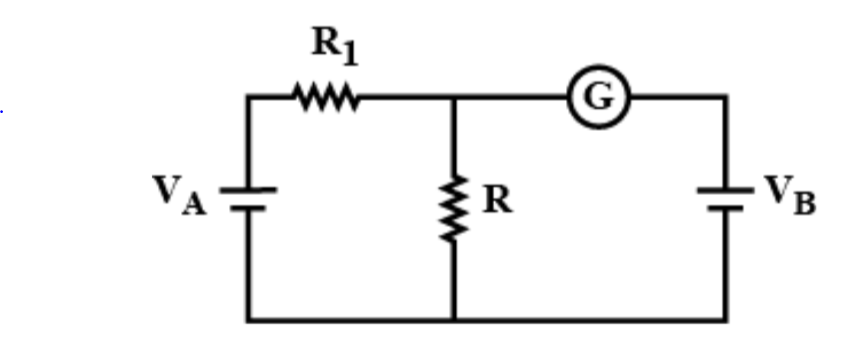
Given: ${V}_{A}=12V$
${R}_{1}=500\Omega$
R=100$\Omega$
According to Ohm’s Law,
$V=IR$ …(1)
For the loop with ${V}_{A}$, the current across two resistors in series is given by,
$I= \dfrac {{V}_{A}}{{R}_{1} +R}$
Substituting the values in above equation we get,
$I= \dfrac {12}{500 +100}$
$\therefore I= \dfrac {12}{600}$
$\therefore I= 0.02A$
Voltage between R and ${R}_{1}$ can be calculated by substituting the values in equation.(1).
Thus, the voltage between R and ${R}_{1}$ can be given as,
$V= 0.02 \times 100$
$\therefore V= 2V$
Thus, the value of ${V}_{A}$ is 2V.
Hence, the correct answer is option D i.e. 2V.

Note: As there is no deflection in the galvanometer, we can say there is no current flow through the galvanometer. There is no flow of current because both the ends of the galvanometer have equal potential which makes a potential difference to be zero. The galvanometer is always connected in series so that we can determine the exact value of current in the circuit.
Current in the loop with ${V}_{A}$ can also be calculated using Kirchhoff’s Law.
Using Kirchhoff’s law,
$RI + {R}_{1}I= V$
Substituting the values in above equation we get,
$100I +500I=12$
$\Rightarrow 12= 600I$
$\Rightarrow I= 0.02V$