Question

In the circuit shown, the capacitor ${{C}_{1}}$ has an initial charge ${{q}_{0}}=10\mu C$. When the switch $S$ is closed, and steady state is reached,

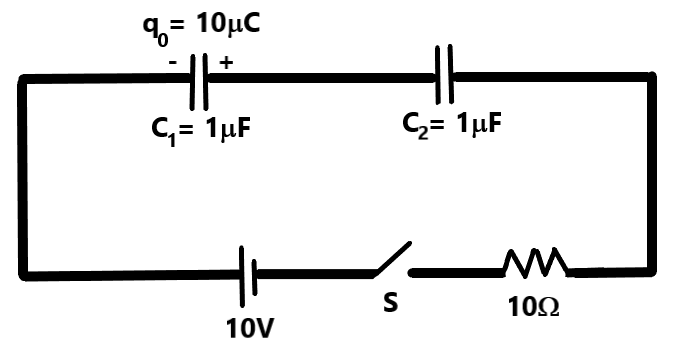
$1)$work done by cell is $100\mu J$
$2)$amount of energy dissipated through resistor is $100\mu J$
$3)$Charge on ${{C}_{1}}$ is $10\mu C$
$4)$Charge on ${{C}_{2}}$ is $0\mu C$
Select the correct statement
$\begin{aligned} & A)1,2 \\\ & B)1,3 \\\ & C)2,4 \\\ \end{aligned}$
$D)$None of these

Answer 1

The given capacitors in the circuit are connected in series. Equivalent capacitance of capacitors connected in series is deduced. With this equivalent capacitance, work done by the cell as well as the energy dissipated through the resistor is determined. In an $RC$ circuit, work done by the cell, energy dissipated through the resistor and the energy stored in the capacitor are equal.
Formula used:
$1)\dfrac{1}{C}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}+\dfrac{1}{{{C}_{3}}}+...+\dfrac{1}{{{C}_{n}}}$
$2)E=\dfrac{1}{2}QV$
$3)E=W={{E}_{r}}$

Complete answer:
In the circuit given below, it is clear that capacitor ${{C}_{1}}$ and capacitor ${{C}_{2}}$ are connected in series.

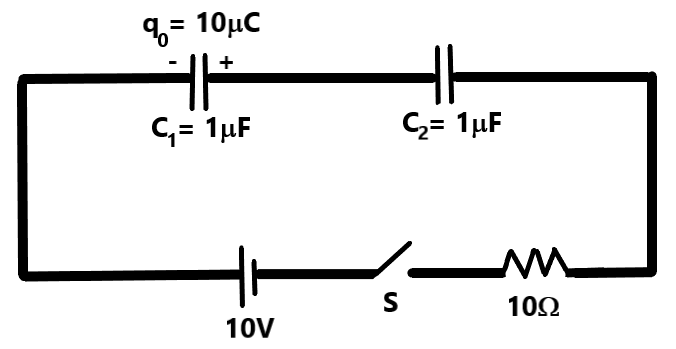
We know that equivalent capacitance of $n$ capacitors connected in series is given by
$\dfrac{1}{C}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}+\dfrac{1}{{{C}_{3}}}+...+\dfrac{1}{{{C}_{n}}}$
where
$n$ is any positive integer
$C$is the equivalent capacitance of $n$ capacitors connected in series
${{C}_{1}},{{C}_{2}},{{C}_{3}},...,{{C}_{n}}$ are the capacitances of $n$ capacitors
Let this be equation 1.
In the given circuit, when the switch $S$ is turned ON and steady state is reached, using equation 1, equivalent capacitance of ${{C}_{1}}$ and ${{C}_{2}}$ is given by
$\dfrac{1}{C}=\dfrac{1}{{{C}_{1}}}+\dfrac{1}{{{C}_{2}}}=\dfrac{1}{1\mu F}+\dfrac{1}{1\mu F}=2\mu F\Rightarrow C=0.5\mu F$
where
$C$ is the equivalent capacitance of ${{C}_{1}}$ and ${{C}_{2}}$ connected in series
${{C}_{1}}={{C}_{2}}=1\mu F$, as provided in the question
Let this be equation 2.
Now, we know that charge stored in a capacitor is given by
$Q=CV$
where
$Q$ is the charge stored in a capacitor when voltage $V$ is applied on the capacitor with capacitance $C$
Let this be equation 3.
Using equation 3, charge stored in the equivalent capacitor of capacitance $C$ in the given circuit is expressed as
$Q=CV=0.5\mu F\times 10V=5\mu C$
where
$Q$ is the charge stored in the equivalent capacitor
$V=10V$ is the applied voltage on the equivalent capacitor
$C$ is the capacitance of the equivalent capacitor
Let this be equation 4.
Here, it needs to be understood that both capacitors in the given circuit store the same charge, which we determined with the help of equivalent capacitance. Therefore,
${{Q}_{1}}={{Q}_{2}}=Q=5\mu C$
where
${{Q}_{1}}$ is the charge stored in capacitor ${{C}_{1}}$
${{Q}_{2}}$ is the charge stored in capacitor ${{C}_{2}}$
$Q=5\mu C$, from equation 4
Let this be equation 5.
Now, let us move on to calculate the energy stored in both the capacitors ${{C}_{1}}$ and ${{C}_{2}}$.
We know that energy stored in a capacitor is given by
$E=\dfrac{1}{2}QV$
where
$E$ is the energy stored in a capacitor
$Q$ is the charge stored in the capacitor
$V$ is the voltage applied to the capacitor
Let this be equation 6.
If ${{E}_{1}}$ and ${{E}_{2}}$ represent the energies stored in capacitors ${{C}_{1}}$ and ${{C}_{2}}$ respectively, using equation 6, the total energy stored in both capacitors $E$ is given by
$E={{E}_{1}}+{{E}_{2}}=\dfrac{1}{2}{{Q}_{1}}V+\dfrac{1}{2}{{Q}_{2}}V=\dfrac{1}{2}V(2Q)=QV=5\mu C\times 10V=50\mu J$
where
$V=10V$, as provided in the question
${{Q}_{1}}={{Q}_{2}}=Q=5\mu C$, from equation 5
Therefore, the total energy stored in capacitors ${{C}_{1}}$ and ${{C}_{2}}$ is equal to $50\mu J$
Now, we know that work done by cell is equal to the energy stored in capacitors ${{C}_{1}}$ and ${{C}_{2}}$.
Clearly,
$W=E=50\mu J$
where
$W$ is the work done by the cell in the given circuit
$E$ is the total energy stored in capacitors ${{C}_{1}}$ and ${{C}_{2}}$
Let this be equation 7.
We also know that energy dissipated through a resistor in the given circuit is equal to the energy stored in the capacitors ${{C}_{1}}$ and ${{C}_{2}}$. Clearly,
${{E}_{R}}=E=50\mu J$
where
${{E}_{R}}$ is the energy dissipated by the resistor in the given circuit
$E$ is the total energy stored in capacitors ${{C}_{1}}$ and ${{C}_{2}}$
Let this be equation 8.

So, the correct answer is “Option D”.

Note:
Students need to be thorough with the formula for equivalent capacitance of capacitors, connected in series. The formula for the same looks very similar to the formula for equivalent resistance of resistors connected in parallel. Any confusion arising here needs to be easily ruled out. Students need to be thorough with the formula for energy stored in the capacitor too. Energy stored in capacitor can also be expressed as
$E=\dfrac{1}{2}QV=\dfrac{1}{2}C{{V}^{2}}$
The second expression in the above equation can also be used to arrive at the required results for the given question.