Question
Question: In the circuit shown, the batteries \({E_1} = {E_2} = 2V\) \({E_3} = 5V\) and the resistances \({R_1...
In the circuit shown, the batteries E1=E2=2V E3=5V and the resistances R1=10Ω,R2=20Ω . The potential difference across the capacitor at the steady state is:
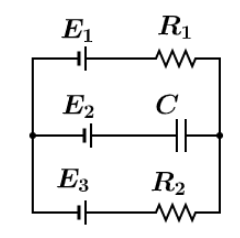
Solution
In electrical circuits consisting of a capacitor, circuits are said to be in steady state when the capacitor is fully charged and no more current flows through the part of the circuit where the capacitor is connected. So, we will find the current flowing in circuit while neglecting the wire consisting E2(and)C and then we will use the general formula between potential difference across two points as V=E−Ir where, E is the net emf and r is the resistance and I is the current flowing across the wire.
Complete step by step answer:
while, neglecting the E2(and)C wire, we have two batteries left of E1=2V and E3=5V , both batteries are facing with their opposite polarity with each other, hence net emf will gets added so net emf between batteries of E1=2V and E3=5V is
Enet=E3−E1
And current is calculated as:
I=RnetEnet
Since, resistances R1=10Ω,R2=20Ω are connected in series so, Rnet=R1+R2 in the case while neglecting E2(and)C wire, so
I=RnetEnet
⇒I=10+205−2
⇒I=303
⇒I=0.1A
Now, consider the only part of circuit consisting of E2(and)C wire and E3=5V wire, we have,
E3=5V
⇒E2=2V
With a resistance r=20Ω
And I=0.1A
net emf can be written as Enet=E3−E2
Enet=3V
Let, V be the potential difference across the capacitor, the we have
V=Enet−Ir
⇒V=3−0.1(20)
∴V=1V
Hence, the potential difference across the capacitor at steady state will be V=1V.
Note: It should be remembered that, while calculating the net emf between two batteries always check the facing polarity of two batteries, if facing polarity are same then net emf will get subtracted and if facing polarity are different net emf will gets added. The relation I=RE is known as Ohm’s law.
