Solveeit Logo
Login

Question

Question: In the circuit shown, the ammeter reading is zero. Then, the value of the resistance R is: ![](htt...

In the circuit shown, the ammeter reading is zero. Then, the value of the resistance R is:

A. 50Ω50\Omega
B. 100Ω100\Omega
C. 200Ω200\Omega
D. 400Ω400\Omega

Explanation

Solution

We are going to apply the concept of Kirchhoff’s Laws to find the voltage is to be used. As there is no current through the ammeter, So the KVL will be applied only to the first loop.

Complete step by step answer:
Kirchhoff’s First Law or Junction rule: In an electric circuit, the algebraic sum of currents at any junction is zero. Or, the sum of currents entering a junction is equal to the sum of currents entering a junction is equal to the sum of currents leaving that junction.
Mathematically, this Law may be expressed as
∑I=0\sum {{\rm I} = 0}
Sign convention for applying junction rule:
1. The current flowing towards the junction is taken as positive.
2. The current flowing away from the junction is taken as negative.
Kirchhoff’s second Law or loop rule: Around any closed loop of a network, the algebraic sum of changes in potential; must be zero. Or, the algebraic sum of emfs in any loop of a circuit is equal to the sum of the products of currents and resistances in it.
First law is also called Kirchhoff’s current law (KCL)
Second law is also called Kirchhoff's voltage law (KVL)
Now, as current through ammeter is zero. So, all the current passing through 500Ω500\Omega resistor passes through R.

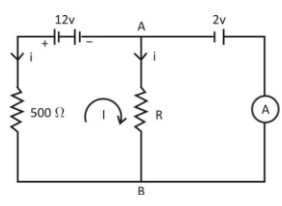
Applying KVL to loop I, we get
500i+12+Ri=0500i + 12 + Ri = 0
Also potential across R is −2V - 2V due to external battery attached
Thus, iR=−2iR = - 2volt
So, equation (I) becomes
500i+12+(−2)=0 500i+10=0 500i=−10 i=−10500 i=−150 A  500i + 12 + \left( { - 2} \right) = 0 \\\ 500i + 10 = 0 \\\ 500i = - 10 \\\ i = \dfrac{{ - 10}}{{500}} \\\ i = \dfrac{{ - 1}}{{50}}{\text{ A}} \\\
Now, iR=−2iR = - 2volt
−150×R=−2 R=−2×−50 R=100Ω  \dfrac{{ - 1}}{{50}} \times R = - 2 \\\ R = - 2 \times - 50 \\\ R = 100\Omega \\\
Hence, option (B) is the correct one.

Note: Remember that while applying KVL, sign conventions is to be followed
Also, iR=−2ViR = - 2V
Because as current flows from A to B according to figure and A is connected to −ve - veterminal of battery while B to positive terminal of battery. So,
VAB=VA−VB{V_{AB}} = {V_A} - {V_B}
=(−)−(+)== \left( - \right) - \left( + \right) =lower value −- higher value
=−ve.= - ve.