Question
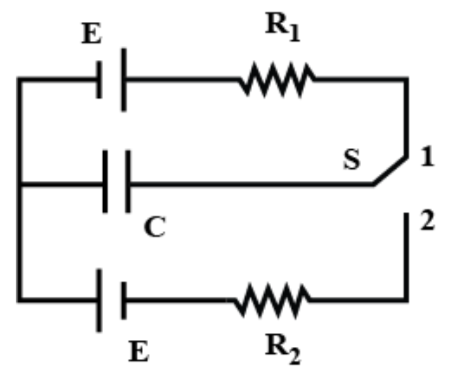
Question: In the circuit shown, switch S is placed in position 1 till the capacitor is charged to half of the ...
In the circuit shown, switch S is placed in position 1 till the capacitor is charged to half of the maximum possible charge in this situation. Now, switch S is placed in position 2. The maximum energy lost by the circuit after switch S is placed in position 2 is:
A). 21CE2
B). 81CE2
C). 87CE2
D). 89CE2
Solution
Find the energy which was stored in the capacitor initially. Then, find the final energy stored in the capacitor. Obtain the expression for work done by the battery. Then, subtract the initial energy from the final energy and subtract the obtained answer from work done by the battery. This will give the maximum energy lost by the circuit.
Complete step-by-step solution:
Initial charge of the capacitor is 2Q
Energy stored in a capacitor is given by,
U=21CQ2 ...(1)
Where Q is the charge
V is the voltage
Substituting value in equation. (1) we get,
UI=21(2Q)2C1
∴UI=81CQ2 ...(2)
But, Q=CE
Substituting this value in the equation. (2) we get,
Ui=81CE2 ...(3)
Final energy stored in the capacitor is given by,
Uf=21CE2
Work done by the battery is
W=(23CE)×E
∴W=23CE2
Heat energy is lost by,
Energy lost=W–(Uf−UI)
Substituting values in above equation we get,
Energy lost= 23CE2−(21CE2−81CE2)
∴ Energy lost= 89CE2
Thus, the maximum energy lost by the circuit is 89CE2.
Hence, the correct answer is option D i.e. 89CE2.
Note: Make sure you write the powers correctly.
The energy stored in the capacitor is electrical energy and not potential energy. An ideal capacitor does not dissipate any of the energy supplied to it. The total energy of a system is always conserved. The lost energy is converted from one form to another by some component in the circuit. In our case, the resistor acts as a medium to expand the energy which was lost by capacitors.
