Question

In the circuit shown, power factor of circuit is $1$ and power factor of box is $\dfrac{3}{5}.$ Find reading of ammeter:

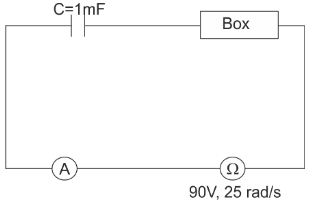
A. $5A$
B. $6A$
C. $4A$
D. $3A$

Answer 1

We know that the power factor of an AC electrical power system is defined as the ratio of the real power absorbed by the load to the apparent power flowing in the circuit, and is a dimensionless number in the closed interval of −1 to 1.Here, power factor is given by $\dfrac{R}{Z}.$ Where, R is resistance and Z is impedance.

Complete step by step answer:
$C = 1mF$, $\omega = 25rad{s^{ - 1}}$ and $V = 90V$.
Now, power factor is given by $= \dfrac{R}{Z}$
Where Z is impedance and is given by $Z = \sqrt {{R^2} + X_c^2}$
Now ${X_c}$ is the capacitive resistance.
${X_c} = \dfrac{1}{{\omega C}}$
Therefore, impedance becomes $Z = {\sqrt {{R^2} + {{\left( {\dfrac{1}{{\omega C}}} \right)}^2}} ^{}}$
Now we have given the power factor of box equal to $\dfrac{3}{5}$
Hence,

\Rightarrow\dfrac{3}{5} = \dfrac{R}{{\sqrt {{R^2} + {{\left( {\dfrac{1}{{25 \times {{10}^{ - 3}}}}} \right)}^2}} }} $$ Now squaring both side we get, $$\dfrac{9}{{25}} = \dfrac{{{R^2}}}{{{R^2} + {{\left( {\dfrac{1}{{25 \times {{10}^{ - 3}}}}} \right)}^2}}}$$ On solving we get, $9{R^2} + 9 \times {40^2} = 25{R^2} \\\ \Rightarrow 9 \times 1600 = 16{R^2} \\\ \Rightarrow R = 30\Omega \\\ $ Since, power factor of circuit is 1 therefore it implies $R = {Z_{eff}}$ Therefore we have, ${Z_{eff}} = 30\Omega $ Hence current through ammeter is $I = \dfrac{V}{{{Z_{eff}}}} \\\ \Rightarrow I = \dfrac{{90}}{{30}} \\\ \therefore I = 3A \\\ $ **Hence option D is correct.** **Note:** Resistance is simply defined as the opposition to the flow of electric current in the circuit. Impedance is opposition to the flow of AC current because of any three components that are resistive, inductive or capacitive. It is a combination of both resistance and reactance in a circuit.