Question

In the circuit shown, $L\quad =\quad 1\mu H$ , $C\quad =\quad 1\mu F$ and $R\quad =\quad 1k\Omega$. They are connected in series with an a.c. source $V\quad ={ V }_{ 0 }\sin { \omega t }$ as shown. Which of the following options is/are correct?

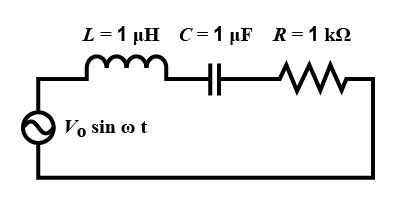
A.)At $\omega \quad >>{ 10 }^{ 6 }\quad rad.{ r }^{ -1 }$, the circuit behaves like a capacitor
B.)At $\omega \sim 0$ the current flowing through the circuit becomes nearly zero.
C.)The current will be in phase with the voltage if $\omega ={ 10 }^{ 4 }rad.{ s }^{ -1 }$
D.)The frequency at which the current will be in phase with the voltage is independent of R.

Answer 1

Use formula for impedance in series LCR circuit. Calculate resonance frequency using impedance formula. This frequency is independent of resistance. Then, use the formula for current in LCR series and let frequency be equal to zero. Thus, current becomes zero.

Formula used:
$Z\quad =\quad R\quad +\quad j\omega L\quad -\dfrac { j }{ \omega C }$
${ \omega }_{ 0 }=\dfrac { 1 }{ \sqrt { LC } }$
$I\quad =\quad \dfrac { V }{ \sqrt { { R }^{ 2 }+\quad { \left( \omega L\quad -\dfrac { 1 }{ \omega C } \right) }^{ 2 } } }$

Complete answer:
When L, R and C are connected in series, impedance is given by,
$Z\quad =\quad R\quad +\quad j\omega L\quad -\dfrac { j }{ \omega C }$ …(1)

Resonant frequency in series LCR circuit is given by,
${ \omega }_{ 0 }=\dfrac { 1 }{ \sqrt { LC } }$
Substituting values in above equation we get,
${ \omega }_{ 0 }=\dfrac { 1 }{ \sqrt { { 10 }^{ -6 }\times { 10 }^{ -6 } } }$
$\therefore \quad { \omega }_{ 0 }=\sqrt { { 10 }^{ -12 } }$
$\therefore \quad { \omega }_{ 0 }=\quad { 10 }^{ 6 }rad$
This obtained value is independent of R.
Now, current I in series LCR circuit is given by,
$I\quad =\quad \dfrac { V }{ \sqrt { { R }^{ 2 }+\quad { \left( \omega L\quad -\dfrac { 1 }{ \omega C } \right) }^{ 2 } } }$
At $\omega \sim 0$, above equations become,
$I\quad =\quad \cfrac { V }{ \infty }$
$\therefore \quad I\quad =\quad 0$
Thus, the current flowing through the circuit becomes zero.

At $\omega \sim 0$ the current flowing through the circuit becomes nearly zero and the frequency at which the current will be in phase with the voltage is independent of R respectively.

So, the correct answer is “Option B and D”.

Note:
When current is in phase with voltage, Impedance (I) becomes equal to resistance (R).
Therefore, the equation. (1) becomes,
$j\omega L\quad =\quad \dfrac { j }{ \omega C }$
$\therefore \quad { \omega }^{ 2 }=\quad \dfrac { 1 }{ LC }$
$\therefore \quad { \omega }=\quad \dfrac { 1 }{ \sqrt { LC } }$