Question

In the circuit shown in the figure, when the input voltage of the base resistance is $10V$, ${{V}_{be}}$ is zero and ${{V}_{ce}}$ is also zero. Value of $\beta$ is
(A). 133
(B). 154
(C). 196
(D). 105

Answer 1

The figure given above shows a transistor with three parts. The current gain is the ratio of the collector current to the ratio of the base current. The emitter and collector current can be calculated by using ohm’s law. The potential can be calculated by taking the difference of potential difference between two points.

Formula used:
${{V}_{i}}-{{V}_{be}}={{I}_{b}}{{R}_{b}}$
${{V}_{CC}}-{{V}_{ce}}={{I}_{c}}{{R}_{c}}$
$\beta =\dfrac{{{I}_{c}}}{{{I}_{b}}}$

Complete step by step solution:

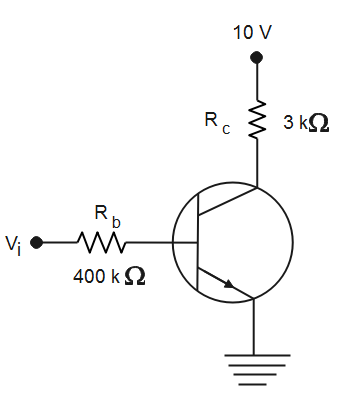
Given that, ${{V}_{be}}=0$, ${{V}_{ce}}=0$. Conditions given in the figure are ${{V}_{i}}=10V$, ${{R}_{b}}=400\times {{10}^{3}}\Omega$, ${{R}_{c}}=3\times {{10}^{3}}\Omega$, ${{V}_{CC}}=10V$.
We know that,
${{V}_{i}}-{{V}_{be}}={{I}_{b}}{{R}_{b}}$
Here, ${{V}_{be}}$ is the voltage of the junction between base and emitter
According to the ohm’s law, ${{I}_{b}}{{R}_{b}}$ is the potential drop across the resistor ${{R}_{b}}$.
Now we will substitute given values in the above equation to get,
$\begin{aligned} & 10-0={{I}_{b}}\times 400\times {{10}^{3}} \\\ & \Rightarrow \dfrac{10}{400\times {{10}^{3}}}={{I}_{b}} \\\ & \Rightarrow 25\times {{10}^{-6}}A=25\mu A={{I}_{b}} \\\ \end{aligned}$
Therefore, the current flowing through the resistance and between ${{R}_{b}}$ is $25\times {{10}^{-6}}A$.
Similarly,
${{V}_{CC}}-{{V}_{ce}}={{I}_{c}}{{R}_{c}}$
Here, ${{V}_{ce}}$ is the voltage between collector-emitter junction
According to ohm’s law, ${{I}_{c}}{{R}_{c}}$ is the potential drop across the resistor ${{R}_{c}}$
Now we will substitute given values in the above equation to get,
$\begin{aligned} & 10-0={{I}_{c}}\times 3\times {{10}^{3}} \\\ & \Rightarrow \dfrac{10}{3\times {{10}^{3}}}={{I}_{c}} \\\ & \Rightarrow 3.33mA={{I}_{c}} \\\ \end{aligned}$
Therefore the current flowing through the resistor ${{R}_{c}}$ is $3.33mA$.
Now,
$\beta =\dfrac{{{I}_{c}}}{{{I}_{b}}}$
Here, $\beta$ is the current gain in the transistor
${{I}_{c}}$ is the collector current
${{I}_{b}}$ is the base current
Given, ${{I}_{c}}=3.33mA$, ${{I}_{b}}=25\mu A$
Now we will substitute given values in the above equation to get,
$\begin{aligned} & \beta =\dfrac{{{I}_{c}}}{{{I}_{b}}} \\\ & \Rightarrow \beta =\dfrac{3.33\times {{10}^{-3}}}{25\times {{10}^{-6}}} \\\ & \Rightarrow \beta =133 \\\ \end{aligned}$
Therefore, the value of current gain in the circuit is $133$. Hence, the correct option is (A).

Note: The transistor contains three parts; the emitter, collector and the base. The current gain is a unitless quantity as it is the ratio of two quantities with similar units. Current gain can be defined as the change in collector current per unit change in the base current. The above circuit is a base-configuration.