Question

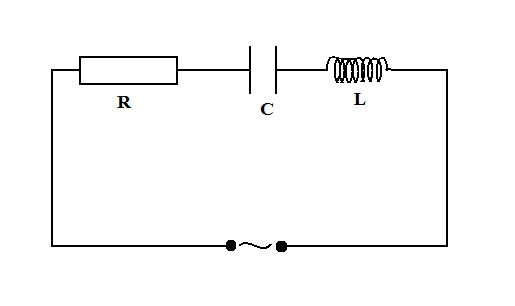
In the circuit shown in the figure, the supply Has a constant $rms$ value $V$ but variable frequency $f$. The frequency at which the voltage drop across $R$ is maximum is( $C = \dfrac{1}{\pi }$ $\mu F$, $L =\dfrac{1}{\pi }$ $H$)

A) $100Hz$.
B) $500Hz$.
C) $300Hz$.
D) None of the above.

Answer 1

Using the formula for voltage of LCR circuits and applying the boundary conditions of resonance, we will be able to calculate the frequency at which voltage drop across $R$ is maximum.

Formula Used:
Formula for voltage of LCR circuits: ${V_R} = R\dfrac{V}{{\sqrt {({R^2} + {{(\omega L - \dfrac{1}{{\omega C}})}^2})} }}$.
Where $R$ is the voltage drop across resistor and is expressed in Volt $(V)$, $V$ is the voltage supplied and is expressed in Volt $(V)$, $L$ inductance and is expressed in Henry $(H)$, $R$ is the resistance value and is expressed in Ohms $(\Omega )$, $C$ is the capacitance value and is expressed in microFarads $(\mu F)$ and $\omega$ is the resonant frequency value and is expressed in Hertz $(Hz)$.

Complete step by step answer:
Relation between frequency and $\omega = 2\pi f$
Where $f$ is the frequency value in any condition and is expressed in Hertz $(Hz)$ $\omega$ is the resonant frequency value and is expressed in Hertz $(Hz)$.
Step by step solution: When the switch is closed, current flows in the circuit due to the battery connected to it. A constant $rms$ value $V$ and a variable frequency $f$is generated.
The voltage drop across the inductor is expressed as ${V_R} = R\dfrac{V}{{\sqrt {({R^2} + {{(\omega L - \dfrac{1}{{\omega C}})}^2})} }}$.
This value of ${V_R}$ will be maximum, that is, equal to the supplied voltage $V$ at resonance condition. In this condition the inductive and capacitive reactances are equal and have a cancelling effect on each other due to their $180^\circ$ phase difference.
Hence, in the above equation, ${V_R}$ will be maximum when $\omega L - \dfrac{1}{{\omega C}} = 0$.
Applying this deduction we get,
$\omega L - \dfrac{1}{{\omega C}} = 0 \\\ \Rightarrow {\omega ^2} = \dfrac{1}{{LC}} \\\$
Applying square root on both sides,
$\omega = \dfrac{1}{{\sqrt {LC} }}$
Substituting the necessary values in resonance condition we get,
$\omega = \dfrac{1}{{\sqrt {\dfrac{1}{\pi } \times {{10}^{ - 6}} \times \dfrac{1}{\pi }} }} \\\ \Rightarrow \omega = \pi \times {10^3}rad \\\ \\\$
We know that $\omega = 2\pi f$
Therefore, substituting the value of $\omega$ from above we get,
$\omega = 2\pi f \\\ \Rightarrow f = \dfrac{\omega }{{2\pi }} = \dfrac{{\pi \times {{10}^3}}}{{2\pi }} \\\ \Rightarrow f = 500Hz \\\$
In conclusion, the correct option is B.

Note: At the boundary condition, that is, resonance the inductive and capacitive reactances are equal and have a cancellation effect on each other due to their $180^\circ$ phase difference. Therefore, they are considered $\dfrac{1}{\pi }$ and not simply $\pi$.