Question

In the circuit shown in the figure, the power which is dissipated as heat in the $6\Omega$ resistor is 6W. What is the value of resistance R in the circuit?

A. $6\Omega$
B. $10\Omega$
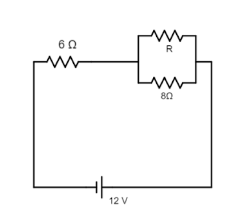
C. $13\Omega$
D. $24\Omega$

Answer 1

We will use the formula for heat dissipated to find the potential difference across the $6\Omega$ resistor and then using this and the current through it we will find the net resistance of the two parallel resistors, then we will use the formula for net resistance of parallel resistors to find the value of R.

Formula used:
Power
$P=IV=\dfrac{{{V}^{2}}}{R}={{I}^{2}}R$
Net resistance of two parallel resistors
$\dfrac{1}{R}=\dfrac{1}{{{R}_{1}}}+\dfrac{1}{{{R}_{2}}}$
Ohm’s law
$V=IR$

Complete answer:
First, we will find the potential difference across the $6\Omega$ resistor. The power is given as 6 Watt for it and using the formula with voltage and resistance, we get
$P=\dfrac{{{V}^{2}}}{R}\Rightarrow V=\sqrt{PR}$
Here P is given as 6 Watt and R is given as $6\Omega$
Then $V=\sqrt{6\times 6}=6$.

Therefore, the potential difference across the $6\Omega$ resistor is 6 V and the remaining 6 V is across the combination of parallel resistors let’s call their net resistance as ${{R}_{net}}$. The current through the whole circuit will be same if we consider ${{R}_{net}}$ and the $6\Omega$ resistors only as they will be in series and the current through two resistors in series is the same, the current through the $6\Omega$ resistor will be
$V=IR\Rightarrow I=\dfrac{V}{R}=\dfrac{6}{6}=1$ Ampere.

This means that the net resistance, ${{R}_{net}}$ can be given by $V=IR\Rightarrow {{R}_{net}}=\dfrac{V}{I}=\dfrac{6}{1}=6\Omega$
Using the formula for the net resistance of a combination of parallel resistors we get

$\begin{aligned} & \dfrac{1}{{{R}_{net}}}=\dfrac{1}{R}+\dfrac{1}{8}\Rightarrow \dfrac{1}{6}=\dfrac{1}{R}+\dfrac{1}{8} \\\ & \Rightarrow \dfrac{1}{R}=\dfrac{1}{6}-\dfrac{1}{8}=\dfrac{8-6}{8\times 6}=\dfrac{2}{48} \\\ & \Rightarrow R=24\Omega \\\ \end{aligned}$

So, the correct answer is “Option D”.

Note:
Take care that instead of finding the resistance of a combination like given in the solution, we can find the total resistance of the system and then subtract the resistance of $6\Omega$ resistor from it. Either way, we would get the same answer.