Question
Question: In the circuit shown in the figure, the power developed across \( 1\Omega ,2\Omega \) and \( 3\Omega...
In the circuit shown in the figure, the power developed across 1Ω,2Ω and 3Ω resistances are in the ratio of
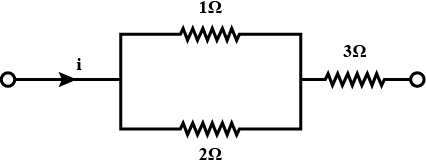
Solution
to solve this question we have to know what the resistance is. Resistance is the measure of the opposition to current flow in an electrical circuit. We know that the unit of resistance is ohm. We know that the symbol of ohm is like a Greek word omega. We know that, when resistance increases then the current flow decreases. Because resistance is inversely proportional to current.
Complete step by step answer:
We can see here, the current in parallel divides in inverse ratio of resistance is
I1=(1+22)i=32i
I2=(1+21)i=31i
Here, we can say according to the question, I is the total current. Now, we can consider P is the power and R is the resistance. P1 is the power developed across 1Ω resistance. Again, P2 is the power developed across 2Ω resistance. Again, P3 is the power developed across the resistance 3Ω .
Now, we know that P=I2R
Now we are going to put the values of resistances which are mentioned in the above question.
Now, P1=I12R=(32)2i2×1=94i2
Again, we can write similarly,
P2=I22R=(31)2i2×2=42i2
Similarly, again, we can write,
P3=I32R=i2×3=3i2
Now, the ratio of the three powers are,
P1:P2:P3=34:92:3=4:2:27
This is the right answer.
Note:
We can get confused between the formula of parallel resistance, series resistances and conductors. We also have to remember that when two resistors are parallel then the potential difference becomes common or same. But when two resistors are connected in a series manner then the current flows through all the resistances are the same or constant.
