Question

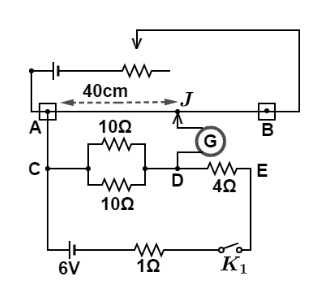
In the circuit shown in the figure, the potential difference between the points $C$ and $D$ is balanced against $40\,cm$ length of potentiometer wire of total length $100\,cm$ In order to balance the potential difference between the points $D$ and $E$, the jockey should be pressed on potentiometer wire at a distance of

A. $16\,cm$
B. $32\,cm$
C. $56\,cm$
D. $80\,cm$

Answer 1

A potentiometer is a device which is used to determine the potential difference across unknown battery by balancing the jockey over the $100cm$ length wire, in order to find the balancing length we use the concept of potential gradient which is the ratio of potential difference per unit of length denoted by $K = \dfrac{V}{l}$.

Complete step by step answer:
Let $V$ be the potential difference across point $C$ and $D$ and length of balancing jockey is ${l_1}$ hence, potential gradient is
$K = \dfrac{{I{R_1}}}{{{l_1}}}$
Now, ${l_2}$ be the length of balancing jockey for the potential difference between points $D$ and $E$ hence, potential gradient is
$K = \dfrac{{I{R_2}}}{{{l_2}}}$
Compare both equations we get,
$\dfrac{{I{R_1}}}{{{l_1}}} = \dfrac{{I{R_2}}}{{{l_2}}}$
$\Rightarrow {l_2} = (\dfrac{{{R_2}}}{{{R_1}}}){l_1}$
Now, ${R_1}$ is the total resistance of net parallel combination of $10\Omega$ each and calculated as:
${R_1} = \dfrac{{10 \times 10}}{{10 + 10}}$
$\Rightarrow {R_1} = 5\Omega$
And, from the figure ${R_2} = 4\Omega$, ${l_1} = 40\,cm$ putting these values we get,
${l_2} = (\dfrac{4}{5})40$
$\therefore {l_2} = 32\,cm$
So, the balancing length of the jockey should be pressed at a distance of ${l_2} = 32\,cm$

Hence, the correct option is B.

Note: It should be remembered that, the parallel combination of two resistances gives the net resistance is calculated by using the formula $\dfrac{1}{{{R_{net}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$ and also, the two $10\Omega$ resistances and the one with $4\Omega$ resistance are connected in series so, same current $I$ passes through both of them.