Question
Question: In the circuit shown in the figure, the potential difference across the \(4.5\mu F\) capacitor is: ...
In the circuit shown in the figure, the potential difference across the 4.5μF capacitor is:
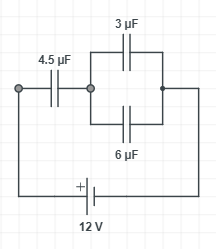
Solution
A capacitor is a two terminal component that stores electrical energy in the form of potential energy, and later discharges them. This property is called the capacitance of the capacitor. Since we are given some combination of capacitor and then use it to find the current through 4.5μF capacitor and then find the potential difference.
Formula used: Q=CV
Complete step by step answer:
A capacitor can store electrical energy, and behaves as a temporary battery. They are used mainly to maintain the power supply while batteries are being changed. It can also store information in the form of binary digits. It is the main component used in full wave and half wave rectifier. (symbol: F), named after the English physicist Michael Faraday. A 1 farad capacitor, when charged with 1 coulomb of electrical charge, has a potential difference of 1 volt between its plates. The series of capacitor is the sum of reciprocal of its individual capacitors, whereas in resistance the parallel is the sum of reciprocal of its individual resistors. Also remember that capacitors can charge and discharge.
The net parallel capacitance is given as CP=3+6=9μF
We can calculate the net capacitance as Cs1=4.51+91=31
CS=3μF
We know that Q=CV where, Q is the charge in the capacitance C due to some voltage V.
Given that, V=12V.
⇒Q=3×10−3×12=36×10−3=36μC
Then the potential across the 4.5μF capacitor is given as V=CQ=4.5×10−336×10−3=8V
So, the correct answer is “Option D”.
Note: The series of capacitors is the sum of reciprocal of its individual capacitors, whereas in resistance the parallel is the sum of reciprocal of its individual resistors. Also remember that capacitors can charge and discharge.
