Question
Question: In the circuit shown in the figure, the input voltage \({v_i}\) is 20 volts, \({V_{BE}} = 0\) and \(...
In the circuit shown in the figure, the input voltage vi is 20 volts, VBE=0 and VCE=0. The values of IB,IC and β are
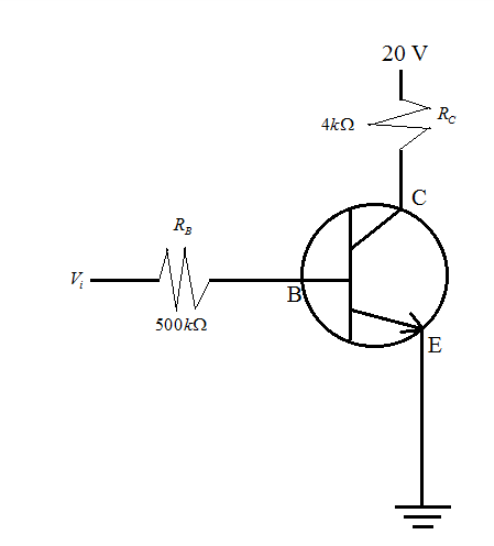
A.IB=20μA,IC=5mA,β=250 B.IB=40μA,IC=10mA,β=250 C.IB=40μA,IC=5mA,β=125 D.IB=25μA,IC=5mA,β=200
Solution
In this question, we need to determine the current through the base and the collector of the transistor. Also, we need to determine the value of β for the given transistor. For this, we will use Kirchhoff's voltage law and properties of the transistors.
Complete step by step answer:
Let IB and IC be the current flowing in the base and the collector of the given transistor.
According to Kirchhoff’s voltage law, the sum of the voltage drop in a closed circuit equals to zero.
So, applying Kirchhoff’s voltage law in the segment from source to the ground.
Vi−VRB−VBE=0 where, Vi,VRB and VBE are the voltage drops across the elements.
The voltage drop across the resistance is the product of the resistance and the current flowing through it. So,
⇒VRB=IB×RB ⇒VRB=IB×500kΩ
Substituting the value of Vi=20, VRB=IB×500kΩ and VBE=0 in the equation Vi−VRB−VBE=0, we get
⇒Vi−VRB−VBE=0 ⇒20−IB×500kΩ−0=0 ⇒IB×500kΩ=20 ⇒IB=500kΩ20 ⇒IB=0.4×10−4A ∴IB=40μA
Hence, the value of the current flowing through the base is 40 micro-amperes.
Again. Following the Kirchhoff’s voltage law for the current flowing through the collector to the ground.
20−VRC−VCE=0
The voltage drop across the resistance is the product of the resistance and the current flowing through it. So,
⇒VRC=IC×RC ⇒VRC=IC×4kΩ
Substituting the value of VRC=IC×4kΩ and VCE=0 in the equation 20−VRC−VCE=0, we get
⇒20−VRC−VCE=0 ⇒20−IC×4kΩ−0=0 ⇒IC×4kΩ=20 ⇒IC=4kΩ20 ⇒IC=5×10−3A ∴IC=5mA
Hence, the value of the current flowing through the collector is 5 milli-amperes.
The ratio of the collector current and the base current of a transistor results in the beta value of the transistor. Mathematically, β=IBIC.
So, substitute the value of base current as 40 micro-amperes and the collector current as 5 milli-amperes in the formula β=IBIC to determine the value of beta.
⇒β=IBIC ⇒β=40μA5mA ⇒β=40×10−65×10−3 ∴β=125
Therefore, IB=40μA,IC=5mA,β=125 is the desired result.
Hence,option C is the correct answer.
Note: It is interesting to be noted here that the value of the ground voltage should always be taken as zero (0). Moreover, there are no elements connected in between the base and the emitter as well as the collector and the emitter and so, we have taken the potential difference as zero.
