Question
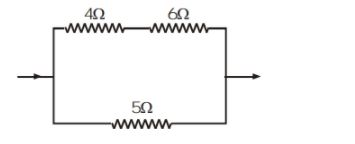
Question: In the circuit shown in the figure the heat produced in the 5ohm resistor due to the current flowing...
In the circuit shown in the figure the heat produced in the 5ohm resistor due to the current flowing through it is 10 calories per second. The heat generated in the 4 ohm resistor is
A. 1calorie/per
B. 2 calorie/per
C. 3 calorie/per
D. 4 calorie/per
Solution
In such a type of question we must know the concept of resistor in series and parallel and the heating effect of electric current and how I and V vary in series and parallel combination.
Formula used - I42R4=(22)2×4=2cal/sec
- H=I2Rt
- V=IR
- Current through a resistor in series combination, IS=R1+R2V
Complete step-by-step answer:
Any resistor in a circuit that has a voltage drop over it dissipates electrical power. This electrical power is converted to heat energy, and thus all resistors have a power rating. The conversion rate is the dissipation power.
Now, it is given that,
Heat generated at 5 ohms resistor=10 calories per second
Heat yielded, H=I2Rt
Here, tH5=I52R5=10⇒I5=510=2, This is the current through the resistor to 5 ohm.
Voltage through 5 ohms resistor V5=I5R5=2×5=52V
As the resistors (4,6) and 5 are parallel, the overall potential (4,6) is equal to that of V5
As the 4 and 6 resistors are so present through each resistor in series I4=I6=4+6V5=4+652=22
Heat produce in resistor 4 per sec,I42R4=(22)2×4=2cal/sec
Hence the correct answer is option B.
Note: In such a type of question, we must apply the formula on the given resistor to obtain V and I in the resistor given and then apply the concept and formula of series and parallel combination for finding the required quantity.
