Question

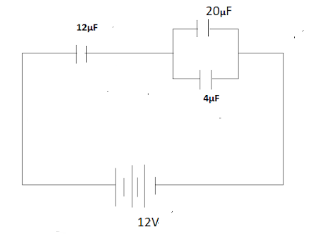
In the circuit shown in the figure, the charge on the capacitor of $4\mu F$ is $16\mu C$ . Calculate the energy stored in the capacitor of $12\mu F$ capacitance.

Answer 1

Hint : In order to solve this question, we are going to first calculate the equivalent capacitances of the two capacitors $20\mu F$ and $4\mu F$ , then, as we are given the charge on the capacitor $4\mu F$ , so, the voltage can be calculated, and as this combination is in series with capacitor $12\mu F$ , and thus, energy is calculated.

Complete Step By Step Answer:
The voltage across the capacitor is given as:
$V = \dfrac{Q}{C}$
Where $Q$ is the charge stored in the capacitor of the capacitance $C$ , $V$ is the voltage
The energy stored in the capacitor is
$E = \dfrac{1}{2}C{V^2}$
Complete step by step solution: Let us start by considering the capacitors, we get
The equivalent capacitance of the capacitors $20\mu F$ and $4\mu F$ is:
$C = 20\mu F + 4\mu F = 24\mu F$
As the charge stored in the capacitor of $4\mu F$ is $16\mu C$ , the voltage across it is:
V = \dfrac{Q}{C} \\\ \Rightarrow V = \dfrac{{16}}{4} = 4V \\\
Thus, the voltage across the capacitors $20\mu F$ and $4\mu F$ is $4V$
As the capacitors $12\mu F$ and the parallel combination of the capacitors $20\mu F$ and $4\mu F$ are in series, so the voltage across the capacitor $12\mu F$ is
$\left( {12 - 4} \right)V \Rightarrow 8V$
The energy stored in the capacitor of $12\mu F$ capacitance can be calculated using the formula
$E = \dfrac{1}{2}C{V^2}$
Putting the values of the capacitance and the voltage, we get,
E = \dfrac{1}{2} \times 12 \times {\left( 8 \right)^2} \\\ \Rightarrow E = 384J \\\

Note :
It is important to see that the capacitors that are present in series combination have the different voltages while the combination of the capacitors that are present in the parallel combination have the same voltages across them. The energy stored in the capacitors depends on the voltage and the capacitance values.