Question
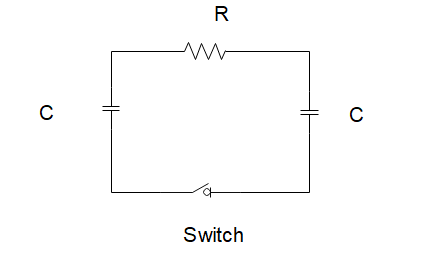
Question: In the circuit shown in the figure the capacitance of each capacitor is equal to \(C\) and resistanc...
In the circuit shown in the figure the capacitance of each capacitor is equal to C and resistance R. One of the capacitors was charged to a voltage V0 and then at the moment t=0 was shorted by means of the switch S.
Find:
(a) the current in the circuit as a function of time t
(b) the amount of generated heat
Solution
In this solution, we will use Kirchhoff’s voltage law to determine the equation of current in the circuit. The heat generated will depend on the current in the circuit and on the value of the resistance.
Formula used:
In this solution, we will use the following formula:
- Voltage difference across resistor: V=iR where i is the current in the circuit and R is the value of the resistance
- Voltage difference across capacitor: V=CQ
- Current due to flow of charge: i=dtdQ .
Complete step by step answer
In the circuit given to us, one of the capacitors has been charged to a voltage V0 . Hence its charge will be:
⇒Q0=CV0
Now when the switch is shorted, the capacitor will flow charge in the system eventually charging the other capacitor and losing energy in the resistor.
The equation of current in the circuit can be determined from Kirchhoff’s voltage law as ∑V=0
For a capacitor, the voltage difference across it will be V=Q/C . Let the charge in the circuit at time t be Q . Then for the initially-charged capacitor, the voltage difference across it will be
⇒CQ0−Q .
And for the initially uncharged capacitor, the voltage difference will be CQ . So, we can write the Kirchhoff’s voltage law as
⇒CQ0−Q−iR=CQ
As i=dtdq , we can write
⇒CQ0−2Q=dtdQR
ON taking the charge terms on one side, we can write
⇒Q0−2QdQ=RC1dt
On integrating both sides for the charge of Q=CV0 to Q=0 in time t=0 to t=∞ , we get
⇒Q=2CV01−eRC−2t
Then the current in the circuit as a function of time will be:
⇒i=dtdQ
Substituting the value of Q=2CV01−eRC−2t , we get
⇒i=RV0eRC−2t
Hence this is the current flowing in the circuit at a time t .
Now to find the heat generated in the system, we can calculate it as
⇒H=t=0∫∞i2Rdt
Substituting the value of i=RV0eRC−2t and integrating with respect to time, we get
⇒H=RV02eRC−4tt=0t=∞×RC
Which gives us
⇒H=41V02C which is the heat generated in the system.
Note: While calculating the heat generated in the system, we cannot directly multiply the time interval since the time interval is infinite which is why the heat generated has to be calculated in one small time frame and has to be integrated. We should know that in this equation, since there is no constant power input, and resistance is present, the current in the circuit will eventually decay to zero which will help us in defining the initial and final limits of the current.
