Question

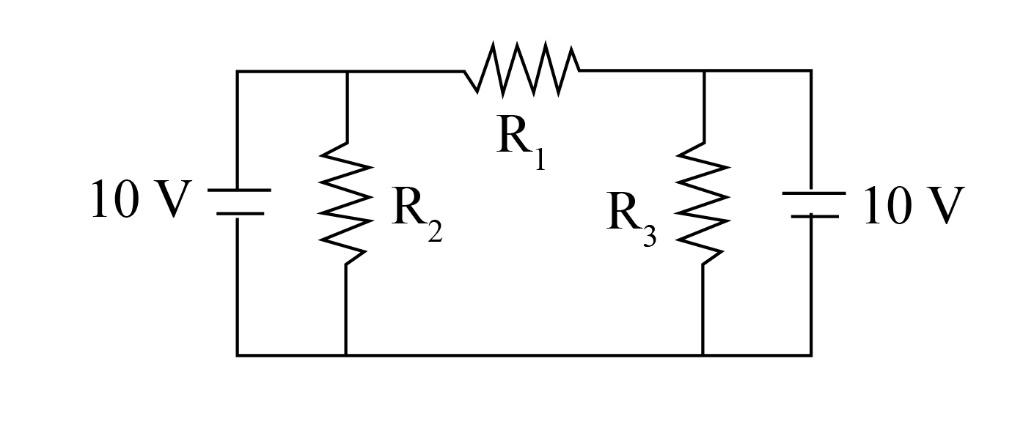
In the circuit shown in the figure, ${R_1} = {R_2} = {R_3} = 10{\rm{ }}\Omega$. Find the currents through ${R_1}$ and ${R_2}$.

Answer 1

From the concept of Ohm’s law, we can say that if a resistor of resistance R is subjected is to a power supply of potential V then the potential difference across that resistor is linearly proportional to the resistance of that resistor.
Complete step by step answer:
Given:
The resistance of all resistors is the same and given as ${R_1} = {R_2} = {R_3} = 10{\rm{ }}\Omega$.

We have to find the value of current through ${R_1}$ and ${R_2}$.

From the given figure we can see that two power supplies of $10{\rm{ V}}$ potential each are connected in the same direction. Therefore, the potential difference across ${R_1}$ and ${R_2}$ is equal to the summation of the potential of both the power supplies.

V = 10{\rm{ V}} + {\rm{10 V}}\\\ = 20{\rm{ V}} \end{array}$$ Let us write the expression for current across the resistor of resistance $${R_1}$$ is equal to the ratio of potential difference and resistance of that resistor. $${I_1} = \dfrac{V}{{{R_1}}}$$ Substitute $$10{\rm{ }}\Omega $$ for $${R_1}$$ and $$20{\rm{ V}}$$ for V in the above expression. $$\begin{array}{c} {I_1} = \dfrac{{20{\rm{ V}}}}{{10{\rm{ }}\Omega }}\\\ = 2{\rm{ A}} \end{array}$$ Write the expression for current across the resistor of resistance $${R_2}$$ is equal to the ratio of potential difference and resistance of that resistor. $${I_2} = \dfrac{V}{{{R_2}}}$$ Substitute $$10{\rm{ }}\Omega $$ for $${R_2}$$ and $$20{\rm{ V}}$$ for V in the above expression. $$\begin{array}{c} {I_1} = \dfrac{{20{\rm{ V}}}}{{10{\rm{ }}\Omega }}\\\ = 2{\rm{ A}} \end{array}$$ Therefore, we can conclude that the value of current across $${R_1}$$and $${R_2}$$ is the same and equal to $$2{\rm{ A}}$$. **Note:** Current flowing in an electric circuit is divided in the circuit but the value of current coming out the power supply is equal to the value of current going back into it. if a resistor is connected with two power supplies, then potential difference across it is equal to the summation of the potential of both the power supplies.