Question

In the circuit shown in the figure, one of the three switches is kept closed and other two are open. The value of resistance is R = 20 Ω. When the angular frequency(w) of the 100 V source is adjusted to 500 rad/s, 1000 rad/s and 2000 rad/s it was found that the current I was 4A, 5A and 4A respectively. (a) Which switch id closed? ($S_1$, $S_2orS_3$) (b)Find the value of L and C.

Answer 1

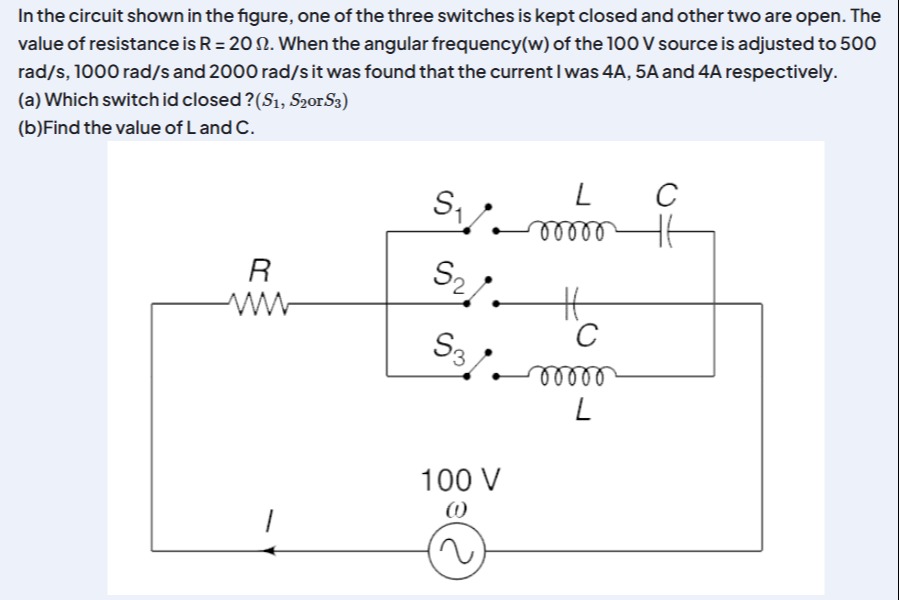
a) The closed switch is $S_1$. b) The values are $L = 0.01$ H and $C = 100 \, \mu$F.

Answer 2

The problem describes an AC circuit with a resistor R and a selectable reactive component (or combination). We are given the resistance R, the source voltage V, and the current I at three different angular frequencies ω.

Part (a): Which switch is closed?

First, let's calculate the impedance (Z) of the circuit at each given angular frequency using Ohm's Law for AC circuits, $Z = V/I$. Given $V = 100$ V and $R = 20$ Ω.

1. At $\omega_1 = 500$ rad/s, $I_1 = 4$ A. $Z_1 = \frac{V}{I_1} = \frac{100}{4} = 25 \, \Omega$.

2. At $\omega_2 = 1000$ rad/s, $I_2 = 5$ A. $Z_2 = \frac{V}{I_2} = \frac{100}{5} = 20 \, \Omega$.

3. At $\omega_3 = 2000$ rad/s, $I_3 = 4$ A. $Z_3 = \frac{V}{I_3} = \frac{100}{4} = 25 \, \Omega$.

Notice that at $\omega_2 = 1000$ rad/s, the impedance $Z_2 = 20 \, \Omega$, which is equal to the resistance R. This condition ($Z=R$) occurs at resonance in an RLC circuit. Let's analyze each switch configuration:

• If Switch $S_1$ is closed: The circuit is a series RLC circuit. The impedance is given by $Z = \sqrt{R^2 + (X_L - X_C)^2}$, where $X_L = \omega L$ and $X_C = \frac{1}{\omega C}$. At resonance, $X_L = X_C$, which means $\omega L = \frac{1}{\omega C}$, and the impedance becomes $Z = R$. Since $Z_2 = R$ at $\omega_2 = 1000$ rad/s, this indicates that the circuit is in resonance at this frequency. This is consistent with $S_1$ being closed.

• If Switch $S_2$ is closed: The circuit is an RC series circuit (R in series with C). The impedance is given by $Z = \sqrt{R^2 + X_C^2} = \sqrt{R^2 + \left(\frac{1}{\omega C}\right)^2}$. For $Z$ to be equal to $R$, $X_C$ must be zero, which implies $1/(\omega C) = 0$, meaning $C \to \infty$. This is not a practical capacitor. Thus, $S_2$ cannot be the closed switch.

• If Switch $S_3$ is closed: The circuit is an RL series circuit (R in series with L). The impedance is given by $Z = \sqrt{R^2 + X_L^2} = \sqrt{R^2 + (\omega L)^2}$. For $Z$ to be equal to $R$, $X_L$ must be zero, which implies $\omega L = 0$, meaning $L=0$. This is not a practical inductor. Thus, $S_3$ cannot be the closed switch.

Therefore, the only consistent option is that Switch $S_1$ is closed.

Part (b): Find the value of L and C.

Since $S_1$ is closed, the circuit is a series RLC circuit. From Part (a), we know that the circuit is in resonance at $\omega_0 = 1000$ rad/s. At resonance, $\omega_0 L = \frac{1}{\omega_0 C}$. This gives us the relationship: $\omega_0^2 = \frac{1}{LC}$ $(1000)^2 = \frac{1}{LC}$ $10^6 = \frac{1}{LC} \implies LC = 10^{-6}$ (Equation 1)

Now, let's use the impedance at another frequency, for example, $\omega_1 = 500$ rad/s, where $Z_1 = 25 \, \Omega$. $Z_1^2 = R^2 + \left(\omega_1 L - \frac{1}{\omega_1 C}\right)^2$ $25^2 = 20^2 + \left(500 L - \frac{1}{500 C}\right)^2$ $625 = 400 + \left(500 L - \frac{1}{500 C}\right)^2$ $225 = \left(500 L - \frac{1}{500 C}\right)^2$ Taking the square root of both sides: $\pm 15 = 500 L - \frac{1}{500 C}$ (Equation 2)

From Equation 1, we can express $C$ in terms of $L$: $C = \frac{1}{10^6 L}$. Substitute this into Equation 2: $\pm 15 = 500 L - \frac{1}{500 \left(\frac{1}{10^6 L}\right)}$ $\pm 15 = 500 L - \frac{10^6 L}{500}$ $\pm 15 = 500 L - 2000 L$ $\pm 15 = -1500 L$

Since inductance L must be a positive value, we choose the negative sign on the left side: $-15 = -1500 L$ $L = \frac{15}{1500} = \frac{1}{100} = 0.01$ H

Now substitute the value of L back into Equation 1 to find C: $C = \frac{10^{-6}}{L} = \frac{10^{-6}}{0.01} = \frac{10^{-6}}{10^{-2}} = 10^{-4}$ F $C = 100 \times 10^{-6}$ F = 100 μF

Let's quickly verify with $\omega_3 = 2000$ rad/s, where $Z_3 = 25 \, \Omega$. $X_L - X_C = \omega_3 L - \frac{1}{\omega_3 C} = 2000(0.01) - \frac{1}{2000(10^{-4})}$ $= 20 - \frac{1}{0.2} = 20 - 5 = 15$. $Z_3 = \sqrt{R^2 + (15)^2} = \sqrt{20^2 + 15^2} = \sqrt{400 + 225} = \sqrt{625} = 25 \, \Omega$. This matches the given $Z_3$, confirming our values for L and C.

The term $(\omega L - 1/(\omega C))$ is negative for $\omega < \omega_0$ (capacitive) and positive for $\omega > \omega_0$ (inductive). For $\omega_1 = 500$ rad/s ($<\omega_0$), we had $500L - 1/(500C) = -1500L = -15$, which is consistent. For $\omega_3 = 2000$ rad/s ($>\omega_0$), we had $2000L - 1/(2000C) = 15$, which is consistent.

Explanation:

1. Calculate impedance $Z = V/I$ for each frequency.
2. Observe that at $\omega = 1000$ rad/s, $Z = 20 \, \Omega$, which equals the resistance R. This indicates a resonance condition.
3. Analyze the circuit for each switch:
   • $S_1$ closed: Series RLC circuit. Resonance ($Z=R$) is possible when $X_L = X_C$.
   • $S_2$ closed: RC circuit. $Z = \sqrt{R^2 + X_C^2}$. $Z=R$ only if $X_C=0$ (infinite C), which is not physically realistic.
   • $S_3$ closed: RL circuit. $Z = \sqrt{R^2 + X_L^2}$. $Z=R$ only if $X_L=0$ (zero L), which is not physically realistic.
4. Conclude that $S_1$ must be closed.
5. Use the resonance condition $\omega_0^2 = 1/(LC)$ with $\omega_0 = 1000$ rad/s to get $LC = 10^{-6}$.
6. Use the impedance equation $Z = \sqrt{R^2 + (\omega L - 1/(\omega C))^2}$ with one of the other frequency points (e.g., $\omega = 500$ rad/s, $Z=25 \, \Omega$) to form an equation involving L and C.
7. Solve the system of two equations to find L and C.