Question

In the circuit shown in the figure, current measurements of ammeter ${A_1}$ and ${A_2}$ are respectively.

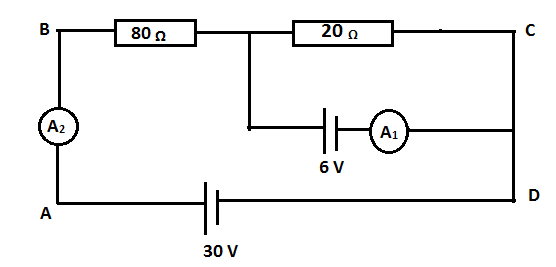
(A) $0A,0.3A$
(B) $0.2A,0.3A$
(C) $0.3A,0.4A$

Answer 1

The first thing we should do here is to identify the nodes or the junction points in the circuit and label each of them. We should also analyze where the current is dividing and label them as $I,{I_1},{I_2}$ accordingly. Now, count the number of loops and apply Kirchhoff’s voltage law in each loop and solve the equations to get the desired value. One should keep Ohm's law into consideration while solving the question.

Complete Step By Step Answer:
We label the nodes or junction points in the circuits with variables $A,B,C,D,E,F{\text{ and }}G$ as shown in the figure.

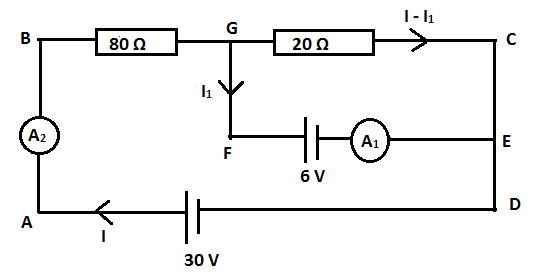
Let $I$ be the current that flows in the loop $ABCD$ . But, as this current $I$ encounters node $G$ , it gets divided into ${I_1}$ in the $GFE$ branch and $I - {I_1}$ in the $GCE$ branch as they are in parallel combination. Therefore, the current measured by ammeter ${A_1}$ will be ${I_1}$ and ammeter ${A_2}$ will measure the current $I$ .
Now, we consider the loop $ABCD$ and apply Kirchhoff’s Voltage Law we get,
$30V = 80I + 20(I - {I_1})$
$\Rightarrow 30V = 100I - 20{I_1}.........(1)$
Similarly, apply Kirchhoff’s Voltage Law in loop $CEFG$ we get,
$6V = 20(I - {I_1})$
$\Rightarrow 6V = 20I - 20{I_1}......(2)$
We have to solve equations (1) and (2) to find the value of two variables $I$ and ${I_1}$ . For that, first, we have to multiple the whole equation (2) by $5$ , we get,
$30V = 100I - 100{I_1}......(3)$
We will now subtract equation (3) from equation (1) we get,
$30V - 30V = (100I - 20{I_1}) - (100I - 100{I_1})$
$\Rightarrow 0 = 80{I_1}$
$\Rightarrow {I_1} = 0A$
Substituting the value of ${I_1}$ in equation (2) we get,
$6V = 20(I - 0)$
$\Rightarrow 6V = 20I$
$\Rightarrow I = 0.3A$
So, option A is the correct answer.

Note:
Both Kirchhoff’s Voltage Law and Kirchhoff’s current law can be applied to solve this type of question.
Kirchhoff’s Voltage Law states that the sum of all the potential differences along a closed loop is zero. While traversing a loop either clockwise or anti-clockwise, if potential increases, put a positive sign in expression and if potential decreases, put a negative sign.
Kirchhoff’s Current law is derived using the law of conservation of charge. It states that the sum of the currents meeting at a point of the circuit is zero i.e. total current entering the circuit is equal to the total current leaving the junction.