Question

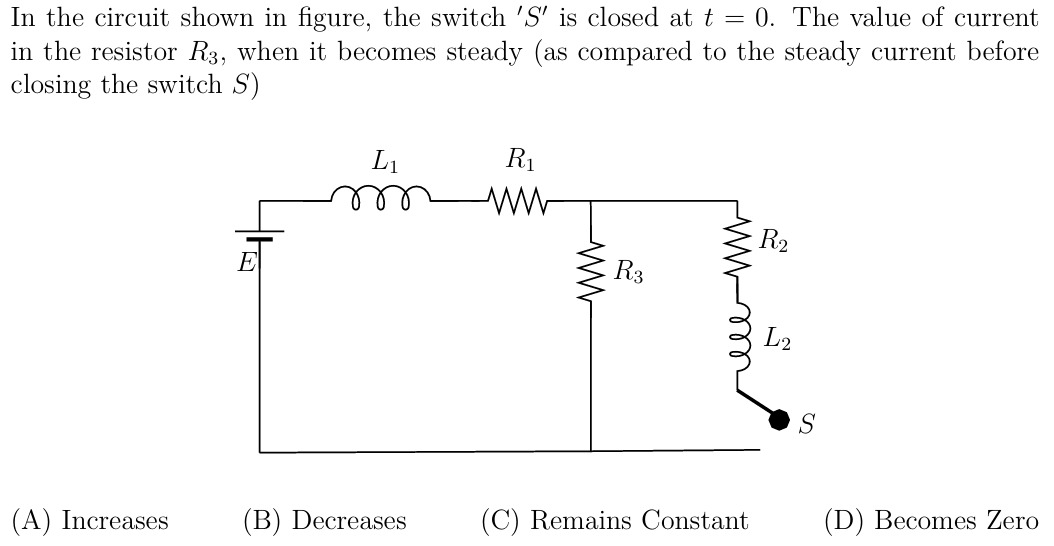
In the circuit shown in figure, the switch 'S' is closed at t = 0. The value of current in the resistor $R_3$, when it becomes steady (as compared to the steady current before closing the switch S)

• A. Increases
• B. Decreases
• C. Remains Constant
• D. Becomes Zero

Answer 1

Answer: (B)

Decreases

Answer 2

To determine the change in current through resistor $R_3$ when the switch 'S' is closed and the circuit reaches a steady state, we need to analyze the circuit in two steady-state conditions: before closing 'S' and after closing 'S'.

Key Concept for Steady State in RL Circuits: In a DC circuit, at steady state, inductors act as short circuits (their resistance is zero because the current is constant, so $L \frac{dI}{dt} = 0$).

1. Before closing switch 'S' (t < 0, steady state):

• The switch 'S' is open, so the branch containing $R_2$, $L_2$, and 'S' is an open circuit and carries no current.
• Inductor $L_1$ acts as a short circuit.
• The circuit effectively consists of the voltage source $E$, resistor $R_1$, and resistor $R_3$ connected in series.

The total resistance of the circuit is: $R_{eq, before} = R_1 + R_3$

The total current drawn from the source is: $I_{total, before} = \frac{E}{R_1 + R_3}$

Since $R_1$ and $R_3$ are in series, the current through $R_3$ is: $I_{R_3, before} = I_{total, before} = \frac{E}{R_1 + R_3}$

The voltage across $R_3$ is: $V_{R_3, before} = I_{R_3, before} \times R_3 = \frac{E R_3}{R_1 + R_3}$

2. After closing switch 'S' (t → ∞, steady state):

• The switch 'S' is closed.
• Both inductors $L_1$ and $L_2$ act as short circuits.
• Now, resistor $R_3$ is in parallel with resistor $R_2$.

The equivalent resistance of the parallel combination of $R_3$ and $R_2$ is: $R_p = \frac{R_3 R_2}{R_3 + R_2}$

It's important to note that for any positive $R_2$ and $R_3$, the equivalent resistance of parallel resistors is always less than the smallest individual resistance. Therefore, $R_p < R_3$.

The total equivalent resistance of the entire circuit is now: $R_{eq, after} = R_1 + R_p = R_1 + \frac{R_3 R_2}{R_3 + R_2}$

Since $R_p < R_3$, it implies: $R_1 + R_p < R_1 + R_3$ So, $R_{eq, after} < R_{eq, before}$

The total current drawn from the source is: $I_{total, after} = \frac{E}{R_{eq, after}}$

Since $R_{eq, after}$ has decreased, the total current drawn from the source must increase: $I_{total, after} > I_{total, before}$

Now, let's find the current through $R_3$ in this new steady state. The voltage across the parallel combination of $R_3$ and $R_2$ (which is also the voltage across $R_3$) is given by: $V_{R_3, after} = I_{total, after} \times R_p$ Also, by Kirchhoff's Voltage Law for the main loop: $V_{R_3, after} = E - I_{total, after} \times R_1$

Since $I_{total, after}$ has increased compared to $I_{total, before}$, the voltage drop across $R_1$ ($I_{total, after} \times R_1$) has increased. As $V_{R_3, after} = E - (\text{increased voltage drop across } R_1)$, it follows that $V_{R_3, after}$ must be less than $V_{R_3, before}$.

Since the voltage across $R_3$ has decreased ($V_{R_3, after} < V_{R_3, before}$), and the resistance $R_3$ itself remains constant, the current through $R_3$ must also decrease: $I_{R_3, after} = \frac{V_{R_3, after}}{R_3}$ Since $V_{R_3, after} < V_{R_3, before}$, then $I_{R_3, after} < I_{R_3, before}$.

Therefore, the value of current in the resistor $R_3$ decreases.