Question

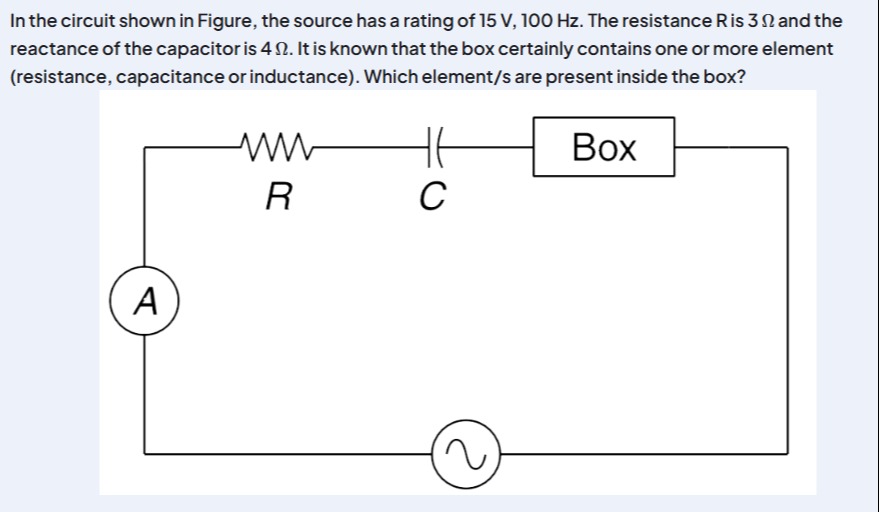
In the circuit shown in Figure, the source has a rating of 15 V, 100 Hz. The resistance R is 3 $\Omega$ and the reactance of the capacitor is 4 $\Omega$. It is known that the box certainly contains one or more element (resistance, capacitance or inductance). Which element/s are present inside the box?

• A. Only a resistor
• B. Only a capacitor
• C. Only an inductor
• D. An inductor and a capacitor

Answer 1

Answer: (C)

Inductor

Answer 2

The circuit shown is a series AC circuit containing a resistor $R$, a capacitor $C$, and a "Box" whose contents are unknown. We are given the following values:

• Source voltage (RMS), $V_{rms} = 15$ V
• Source frequency, $f = 100$ Hz
• Resistance, $R = 3 \, \Omega$
• Reactance of the capacitor, $X_C = 4 \, \Omega$

The problem asks to identify the element(s) present inside the box. The box is known to contain one or more elements (resistance, capacitance, or inductance).

In series RLC circuits, a common special condition is resonance. At resonance, the inductive reactance ($X_L$) equals the capacitive reactance ($X_C$), making the net reactance of the circuit zero. This results in the total impedance being purely resistive, and the current in the circuit being maximum. Given that the ammeter is shown but no specific reading is provided, it is a common practice in such problems to assume the circuit is operating under a "special" condition, and resonance is the most common such condition for series RLC circuits.

Let's assume the circuit is in resonance.
For a series RLC circuit, the total impedance $Z_{total}$ is given by:
$Z_{total} = (R_{total}) + j(X_{L_{total}} - X_{C_{total}})$
where $R_{total}$ is the sum of all resistances, $X_{L_{total}}$ is the sum of all inductive reactances, and $X_{C_{total}}$ is the sum of all capacitive reactances.

In our circuit, we have $R = 3 \, \Omega$ and $X_C = 4 \, \Omega$.
Let the elements inside the box contribute resistance $R_{box}$, inductive reactance $X_{L_{box}}$, and capacitive reactance $X_{C_{box}}$.

The total resistance in the circuit is $R_{total} = R + R_{box} = 3 + R_{box}$.
The total inductive reactance in the circuit is $X_{L_{total}} = X_{L_{box}}$.
The total capacitive reactance in the circuit is $X_{C_{total}} = X_C + X_{C_{box}} = 4 + X_{C_{box}}$.

For resonance, the net reactance of the circuit must be zero:
$X_{L_{total}} - X_{C_{total}} = 0$
$X_{L_{box}} - (4 + X_{C_{box}}) = 0$
$X_{L_{box}} - X_{C_{box}} = 4 \, \Omega$

This equation tells us that the net reactance of the elements inside the box ($X_{box} = X_{L_{box}} - X_{C_{box}}$) must be equal to $4 \, \Omega$.
Since $X_{box}$ is positive, it implies that the inductive reactance inside the box ($X_{L_{box}}$) must be greater than the capacitive reactance inside the box ($X_{C_{box}}$).

Let's consider the possibilities for the elements inside the box based on this condition:

1. If the box contains only a resistor ($R_{box}$): In this case, $X_{L_{box}} = 0$ and $X_{C_{box}} = 0$. The condition becomes $0 - 0 = 4$, which is $0 = 4$, a contradiction. So, the box cannot contain only a resistor.
2. If the box contains only a capacitor ($C_{box}$): In this case, $X_{L_{box}} = 0$. The condition becomes $0 - X_{C_{box}} = 4$, which means $X_{C_{box}} = -4 \, \Omega$. Reactance values are always positive, so this is impossible. Thus, the box cannot contain only a capacitor.
3. If the box contains only an inductor ($L_{box}$): In this case, $X_{C_{box}} = 0$. The condition becomes $X_{L_{box}} - 0 = 4$, so $X_{L_{box}} = 4 \, \Omega$. This is a valid possibility. If the box contains only an inductor with reactance $4 \, \Omega$, the circuit will be in resonance.
4. If the box contains a resistor and an inductor ($R_{box}, L_{box}$): The condition $X_{L_{box}} - X_{C_{box}} = 4 \, \Omega$ still requires $X_{L_{box}} = 4 \, \Omega$ (since $X_{C_{box}}=0$). This is a valid possibility.
5. If the box contains a resistor and a capacitor ($R_{box}, C_{box}$): This leads to the same contradiction as case 2.
6. If the box contains an inductor and a capacitor ($L_{box}, C_{box}$): The condition $X_{L_{box}} - X_{C_{box}} = 4 \, \Omega$ can be satisfied, e.g., $X_{L_{box}} = 5 \, \Omega$ and $X_{C_{box}} = 1 \, \Omega$. This is a valid possibility.
7. If the box contains a resistor, an inductor, and a capacitor ($R_{box}, L_{box}, C_{box}$): The condition $X_{L_{box}} - X_{C_{box}} = 4 \, \Omega$ can be satisfied. This is a valid possibility.

From the analysis, for the circuit to be in resonance, the net reactance of the elements inside the box must be inductive and equal to $4 \, \Omega$. To achieve a net inductive reactance, the box must contain an inductor. It may or may not contain a resistor or a capacitor (as long as $X_{L_{box}} > X_{C_{box}}$ and their difference is $4 \, \Omega$).

Therefore, the only element that is certainly present inside the box, assuming the circuit is at resonance (which is the most common interpretation for such problems when current is not given), is an inductor.