Question
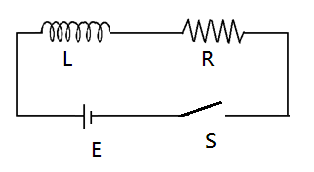
Question: In the circuit shown in figure, switch \(S\) is closed at time \(t = 0\) . The charge that passes th...
In the circuit shown in figure, switch S is closed at time t=0 . The charge that passes through the battery in one-time constant is:
A) LeR2E
B) E(RL)
C) eR2EL
D) EReL
Solution
An inductor and a resistance are connected in the circuit. Current flowing in the LR circuit is given as i=i0(1−e−τt) . The maximum current is given as i0=RE and time τ=RL . Charge is given as q=0∫Tidt . We need to put values of current and time constant and then integrate to get the value of charge passing through the battery.
Complete step by step solution:
We are given an inductor and a resistance which is connected in series to a battery. The connected switch S is closed at time t=0 . As soon as the switch is closed the circuit is complete and thus electric current flows in the circuit. As current is charge flowing per unit time, we can find the charge flowing through the battery if we can find the current.
The current flowing in a LR circuit is given as:
i=i0(1−e−τt)-------equation 1
Here, i is the current at any given time t
i0 is the maximum current given by i0=RE
τ is the time constant given as;
τ=RL-----equation 2
As the battery is connected in the circuit this condition is known as growth of current.
We know that current can be given as:
i=dtdq
Where dq is the amount of charge flowing through time dt
⇒dq=idt
We need to find this charge. We have the value of current, substituting the value of current from equation 1 , we get
⇒dq=i0(1−e−τt)dt
But i0=RE E is the voltage of the battery and R is the resistance;
⇒dq=RE(1−e−τt)dt
The charge at t=0 will be zero. Let the charge be q at some time τ
Thus, integrating the above equation, we get
⇒0∫qdq=RE0∫τ(1−e−τt)dt
Integrating this, we get
⇒q=eR2EL
as ∫e−a=−ae−a
⇒q=RE[τ+eτ−τ](applying limits)
⇒q=RE×eτ
equation 2 we have τ=RL
⇒q=RE×ReL
⇒q=eR2EL
Therefore, the charge that passes through the battery in one-time constant is q=eR2EL
Thus, option C is the correct option.
Note: As soon as the switch is closed charge starts to flow in the circuit. The inductor initially is at very high resistance but as energy is going into building up a magnetic field. Once the magnetic field is up and no longer changing, the inductor acts like a short circuit the time taken for the inductor to fully charge is known as time constant. Therefore, we have taken the upper limit of time as the value of time constant.
