Question
Question: In the circuit shown in figure reading of voltmeter is\[{V_1}\]when only\[{S_1}\]is closed. The read...
In the circuit shown in figure reading of voltmeter isV1when onlyS1is closed. The reading of voltmeter isV2when onlyS2is closed. The reading of voltmeter isV3when bothS1andS2are closed. Then,
A) V2>V1>V3
B) V3>V2>V1
C) V3>V1>V2
D) V1>V2>V3
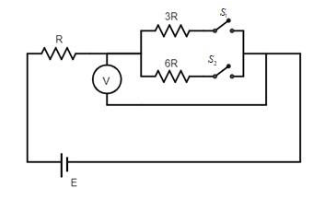
Solution
In case of the closed circuit, we use Kirchhoff's voltage law to find the potential flowing through the given closed circuit.
Complete step by step answer:
Kirchhoff’s law:
Kirchhoff’s voltage law states that “the algebraic sum of the product of current and resistance of the closed circuit is equal to the total EMF provided in the circuit. The symbol of the product of current and resistance depends upon the direction of the current flow in the circuit.
By applying this law we can solve the given problem
(i) The voltmeter reads the valueV1when only the switchS1is closed. Applying Kirchhoff’s voltage law in the given circuit in which only the switchS1is closed. Therefore,
⇒3IR+IR=E
⇒4IR=E
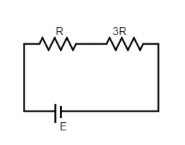
∴I=4RE
Now we can find the value of the potential through the resistance 3R is,
⇒V1=IR
⇒V1=4RE×3R
∴V1=43E--------(1)
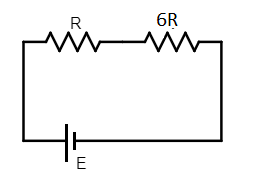
(ii) The voltmeter reads the valueV2when only the switchS2is closed. In this case, on applying Kirchhoff’s voltage law we get,
⇒6IR+IR=E
⇒7IR=E
∴I=7RE
Therefore the voltage through the resistance 6R is,
⇒V2=7RE×6R
∴V2=76E -------------- (2)
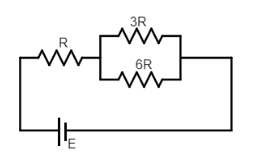
(iii) The voltmeter reads the value V3when both switches are closed. Kirchhoff's law is applied in this case and the two resistances 3R and 6R are in parallel now. Hence the net resistance for the parallel loop is
⇒31+61=63
⇒2R
The Kirchhoff’s law is applied in this case,
⇒IR+2IR=E
⇒3IR=E
∴I=3RE
The voltage flows when both switches are closed,
⇒V3=3RE×2R
∴V3=32E ------------- (3)
From (1), (2) & (3), we can say that theV2>V1>V3.
Hence option A is the correct answer.
Note:
Ohm’s law states that the potential difference across two points is directly proportional to the current flowing through the resistance R. Using Ohm’s law, we are able to find the value of the voltage across any resistance R. Kirchhoff's voltage law is used to find the value of the voltage in the closed circuit.
