Question
Question: In the circuit shown in figure, potential difference between A and B is A. \(30V\) B. \(60V\) ...
In the circuit shown in figure, potential difference between A and B is
A. 30V
B. 60V
C. 10V
D. 90V
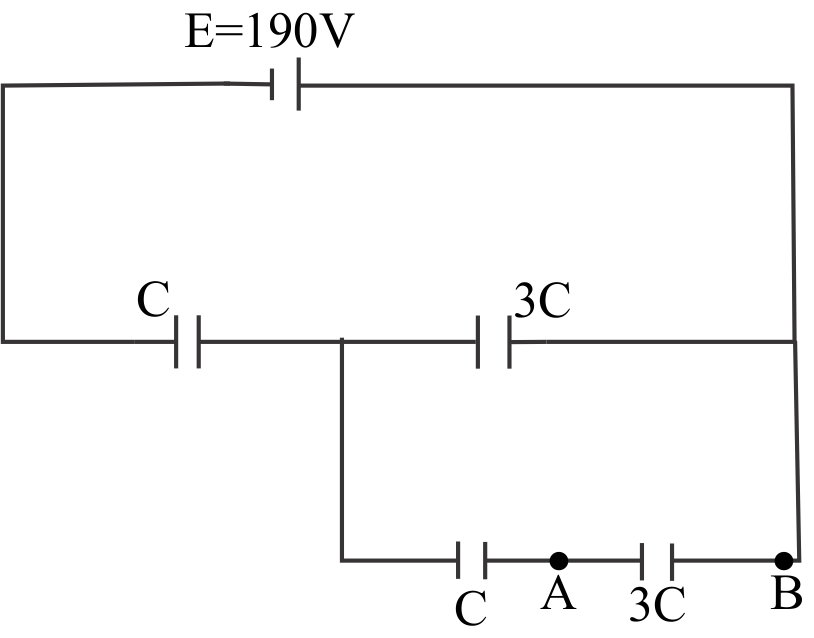
Solution
Hint First calculate the resultant capacitance of the circuit. Then using the appropriate formula, determine its charge. Considering the charge of two capacitors connected in series are the same, calculate the voltage difference across capacitors C and 3C.
Formula used
For series connection, Ceq=C1+C2C1C2 and for parallel connection, Ceq=C1+C2
q=CV where q is the charge of the capacitor, C is called the capacitance and V is the potential difference across the capacitor.
Complete step by step answer
A capacitor is a system of conductors and dielectric that can store electric charge. It consists of two conductors containing equal and opposite charges and has a potential difference V between them.
The potential difference between the conductors is proportional to the charge on the capacitor and is given by the relation q=CV where q is the charge on the positive conductor and C is called the capacitance.
First let us calculate the equivalent capacitance of this circuit.
So,
3+(43) =415
This is the capacitance of the two branches in parallel to each other where 43is the equivalent capacitance of capacitors C and 3C connected in series.
This is in series connection with the capacitance C
So, equivalent capacitance of the circuit is
1+415415= 419415=1915
Using the formula q=CVwe find,
q=1915×190=150C
So, the charge of the resultant capacitance is 150C
Now, as both capacitances 1 and 415 are in series, they must have the same charges.
Therefore, voltage across capacitance 415 is
V=Cq=415150=40V
From the diagram we can show that the voltage across capacitances C and 3C is 40V.
Again since these two capacitors are in series so they must have the same charges.
Equivalent capacitance of Cand 3Cis
Ceq=43
q=CeqV ⇒q=43×40=30C
Therefore the voltage across capacitance 3Cis 330=10V
Thus, the correct option is C.
Note It is important to note that two or more capacitors in series will always have the same charge across their plates. As the charge is equal and constant, the voltage drop across the capacitor is determined by the value of the capacitor only.
