Question

In the circuit shown in figure $\mathop E\nolimits_1 = 7$, $\mathop E\nolimits_2 = 7$, $\mathop R\nolimits_1 = \mathop R\nolimits_2 = 1\Omega$ and $\mathop R\nolimits_3 = 3\Omega$ respectively. The current through the resistance $\mathop R\nolimits_3$ is:

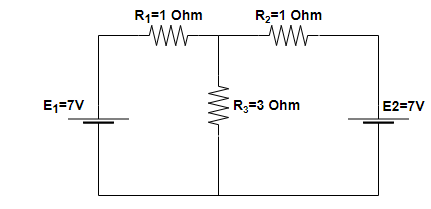
(A) 2A
(B) 3.5A
(C) 1.75A
(D) None of these

Answer 1

The given problem can be seen as a problem based on the combination of cells. For solving these types of problems, the whole circuit is divided into different-different loops and using KVL (Kirchhoff’s Voltage Law) or KCL (Kirchhoff’s Current Law) in these loops’ measurements are done.

Complete step by step answer:
Step 1:

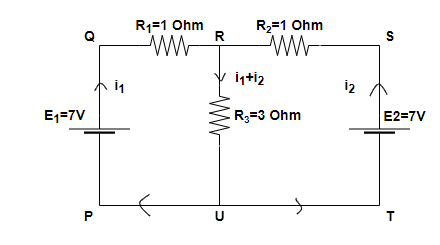
In the above figure, it can be seen that the current flowing into the circuit because of the voltage source $\mathop E\nolimits_1$ is $\mathop i\nolimits_1$ and because of the voltage source$\mathop E\nolimits_2$ is $\mathop i\nolimits_2$.
Using the KVL in the loop PQRUP –
$\mathop E\nolimits_1 - \mathop i\nolimits_1 \mathop R\nolimits_1 - \left( {\mathop i\nolimits_1 + \mathop i\nolimits_2 } \right)\mathop R\nolimits_3 = 0$
Now, using the given values in the above equation
$7 - 1 \times \mathop i\nolimits_1 - \left( {\mathop i\nolimits_1 + \mathop i\nolimits_2 } \right) \times 3 = 0$
Now on rearranging the equation
$7 - 1 \times \mathop i\nolimits_1 - 3 \times \mathop i\nolimits_1 - 3 \times \mathop i\nolimits_2 = 0$
$4 \times \mathop i\nolimits_1 + 3 \times \mathop i\nolimits_2 = 7$ (1)

Step 2: Similarly, using KVL in loop PQRSTUP –
$\mathop E\nolimits_1 - \mathop i\nolimits_1 \mathop R\nolimits_1 + \mathop i\nolimits_2 \mathop R\nolimits_2 - \mathop E\nolimits_2 = 0$
Now using the given values in above equation
$7 - \mathop {1 \times i}\nolimits_1 + 1 \times \mathop i\nolimits_2 - 7 = 0$; on solving this equation
$\mathop i\nolimits_1 = \mathop i\nolimits_2$ (2)
Now substituting the values from equation (2) into equation (1), we will get –
$4 \times \mathop i\nolimits_1 + 3 \times \mathop i\nolimits_1 = 7$ on solving this equation
$\mathop i\nolimits_1 = \mathop i\nolimits_2 = 1$A

Step 3: So, the total current flowing in the branch containing the resistance $\mathop R\nolimits_3$ is equal to the sum of the currents flowing through it because of both the voltage sources $\mathop E\nolimits_1$ and $\mathop E\nolimits_2$ i.e., $\mathop i\nolimits_1$and $\mathop i\nolimits_2$ respectively.
So, $\mathop i\nolimits_3 = \mathop i\nolimits_1 + \mathop i\nolimits_2$
$\mathop i\nolimits_3 = 2$A

$\therefore$ Hence, option (A) is correct.

Note:
(i) While solving this question, we have to take the loop PQRUP and loop PQRSTUP into consideration. If we will take loop PQRUP and loop RSTUR then these two loops will give the identical equations for KVL. So, after solving these identical equations we will have $0 = 0$ from and not able to calculate the values for currents flowing in the circuit i.e., $\mathop i\nolimits_1$and $\mathop i\nolimits_2$ .
(ii) This problem can also be solved by the ‘Superposition Theorem’. It states that for a linear system the response (voltage or current) in any branch of a bilateral linear circuit having more than one independent source equals the algebraic sum of the response caused by each independent source.