Question
Question: In the circuit shown in figure, find the current in inductor as a function of time. ...
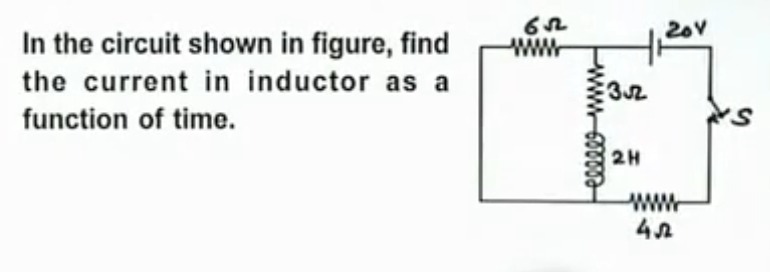
In the circuit shown in figure, find the current in inductor as a function of time.
920(1−e−1027t)
Solution
To find the current in the inductor as a function of time, we use the formula for current growth in an RL circuit:
I(t)=If(1−e−t/τ)
where If is the final (steady-state) current through the inductor and τ is the time constant of the circuit.
1. Calculate the steady-state current (If) through the inductor:
At steady state (t→∞), an inductor acts as a short circuit (its resistance becomes zero). The circuit simplifies as follows:
- The 2H inductor is shorted. The branch containing the 3Ω resistor and the inductor now has a total resistance of 3Ω.
- This 3Ω branch is in parallel with the 6Ω resistor. The equivalent resistance of this parallel combination (Rp) is: Rp=6Ω+3Ω6Ω×3Ω=918=2Ω
- This parallel combination (2Ω) is in series with the 4Ω resistor and the 20V voltage source. The total equivalent resistance of the circuit at steady state (Rtotal) is: Rtotal=4Ω+Rp=4Ω+2Ω=6Ω
- The total current drawn from the source (Isource) is: Isource=RtotalV=6Ω20 V=310 A
- This source current Isource flows through the 4Ω resistor and then splits between the 6Ω resistor and the 3Ω resistor branch (where the inductor is). We need the current through the inductor branch (If). Using the current divider rule: If=Isource×Rother_branch+Rinductor_branchRother_branch If=310 A×6Ω+3Ω6Ω=310×96=310×32=920 A
2. Calculate the Thevenin equivalent resistance (Rth) seen by the inductor:
To find Rth, we deactivate the independent voltage source (replace it with a short circuit) and look into the terminals where the inductor is connected.
- Remove the 2H inductor from the circuit. The 3Ω resistor is in series with the inductor.
- Short the 20V voltage source.
- Now, looking into the terminals where the 2H inductor was connected (i.e., across the 3Ω resistor), the 6Ω resistor is in parallel with the 4Ω resistor. Rparallel′=6Ω+4Ω6Ω×4Ω=1024=2.4Ω
- This equivalent resistance (Rparallel′) is in series with the 3Ω resistor that is directly connected to the inductor.
- Therefore, the Thevenin equivalent resistance seen by the inductor is: Rth=3Ω+Rparallel′=3Ω+2.4Ω=5.4Ω=527Ω
3. Calculate the time constant (τ):
The time constant for an RL circuit is given by τ=RthL. Given L=2 H.
τ=5.4Ω2 H=5420=2710 s
4. Formulate the current as a function of time:
Substitute If and τ into the general formula I(t)=If(1−e−t/τ):
I(t)=920(1−e−t/(2710))
I(t)=920(1−e−1027t)
The current in the inductor as a function of time is I(t)=920(1−e−1027t).
Explanation of the solution:
- Steady-state current (If): At t→∞, the inductor acts as a short circuit. Calculate the total equivalent resistance of the circuit to find the total current from the source. Then, use the current divider rule to find the current flowing through the inductor branch.
- Thevenin equivalent resistance (Rth): To find the resistance that the inductor "sees", deactivate the voltage source (short it) and calculate the equivalent resistance across the inductor's terminals. This involves finding the equivalent resistance of the rest of the circuit in series with the internal resistance of the inductor's branch.
- Time constant (τ): Calculate τ=L/Rth.
- Current function: Substitute If and τ into the standard RL circuit charging equation, I(t)=If(1−e−t/τ).
