Question

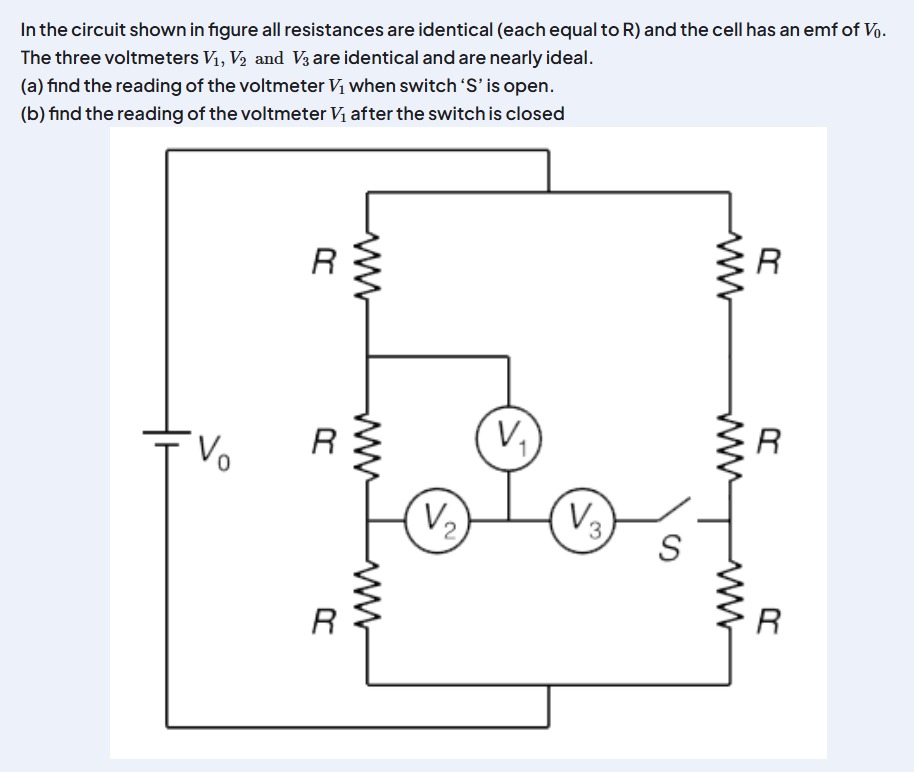
In the circuit shown in figure all resistances are identical (each equal to R) and the cell has an emf of $V_0$. The three voltmeters $V_1$, $V_2$ and $V_3$ are identical and are nearly ideal. (a) find the reading of the voltmeter $V_1$ when switch 'S' is open. (b) find the reading of the voltmeter $V_1$ after the switch is closed

Answer 1

a) V_0/6, b) 2V_0/9

Answer 2

The problem asks for the reading of voltmeter $V_1$ in two scenarios: (a) when the switch 'S' is open, and (b) when the switch 'S' is closed. All resistances are identical (each equal to R), and the cell has an emf of $V_0$. The three voltmeters $V_1$, $V_2$, and $V_3$ are identical and nearly ideal. "Nearly ideal" implies that their internal resistance ($R_V$) is very large but finite, allowing them to establish a potential at the common junction without drawing significant current from the main circuit. Therefore, the current distribution in the resistor branches remains unaffected by the voltmeters.

First, let's determine the potentials at the various nodes in the resistor network. Let the negative terminal of the battery be at 0V and the positive terminal at $V_0$. The circuit consists of two parallel branches, each with three identical resistors (R) in series. The total resistance of each branch is $R_{total} = R + R + R = 3R$. The current flowing through each branch is $I = V_0 / (3R)$.

Let's label the nodes:

• Node $N_1$: Between the top R and middle R on the left side.
• Node $N_2$: Between the middle R and bottom R on the left side.
• Node $N_3$: Between the top R and middle R on the right side.
• Node $N_4$: Between the middle R and bottom R on the right side.

The potentials at these nodes, relative to the 0V terminal, are: $V_{N_1} = V_0 - I \times R = V_0 - (V_0/3R) \times R = V_0 - V_0/3 = 2V_0/3$. $V_{N_2} = V_0 - I \times 2R = V_0 - (V_0/3R) \times 2R = V_0 - 2V_0/3 = V_0/3$. Similarly for the right branch: $V_{N_3} = 2V_0/3$. $V_{N_4} = V_0/3$.

Let J be the common junction point where the voltmeters $V_1$, $V_2$, and $V_3$ meet.

• $V_1$ is connected between $N_1$ and J.
• $V_2$ is connected between $N_2$ and J.
• $V_3$ is connected between $N_4$ and J (through switch S).

Since the voltmeters are identical, they have the same very high internal resistance, say $R_V$.

(a) Find the reading of the voltmeter $V_1$ when switch 'S' is open.

When switch 'S' is open, voltmeter $V_3$ is disconnected from the common junction J. The common junction J is connected to $N_1$ via $V_1$ (resistance $R_V$) and to $N_2$ via $V_2$ (resistance $R_V$). Since no current flows through $V_3$ (it's open), the circuit for determining $V_J$ involves only $V_1$ and $V_2$. This forms a series connection of $V_1$ and $V_2$ between $N_1$ and $N_2$. The potential at J will be the average of the potentials $V_{N_1}$ and $V_{N_2}$, as $V_1$ and $V_2$ are identical (same internal resistance $R_V$). $V_J = \frac{V_{N_1} + V_{N_2}}{2}$ Substitute the calculated potentials: $V_J = \frac{2V_0/3 + V_0/3}{2} = \frac{3V_0/3}{2} = \frac{V_0}{2}$.

The reading of voltmeter $V_1$ is the magnitude of the potential difference between $N_1$ and J: Reading of $V_1 = |V_{N_1} - V_J| = |2V_0/3 - V_0/2|$ To subtract, find a common denominator (6): Reading of $V_1 = |\frac{4V_0}{6} - \frac{3V_0}{6}| = |\frac{V_0}{6}| = \frac{V_0}{6}$.

(b) Find the reading of the voltmeter $V_1$ after the switch is closed.

When switch 'S' is closed, all three voltmeters $V_1$, $V_2$, and $V_3$ are connected to the common junction J. Since the voltmeters are ideal (draw negligible current), the potentials $V_{N_1}, V_{N_2}, V_{N_3}, V_{N_4}$ remain unchanged. $V_{N_1} = 2V_0/3$ $V_{N_2} = V_0/3$ $V_{N_4} = V_0/3$

To find the potential at junction J, we can use Kirchhoff's Current Law (or nodal analysis). The sum of currents leaving junction J through the voltmeters must be zero. Let $I_1, I_2, I_3$ be the currents leaving J through $V_1, V_2, V_3$ respectively. $I_1 = (V_J - V_{N_1}) / R_V$ $I_2 = (V_J - V_{N_2}) / R_V$ $I_3 = (V_J - V_{N_4}) / R_V$ Sum of currents = 0: $I_1 + I_2 + I_3 = 0$ $\frac{V_J - V_{N_1}}{R_V} + \frac{V_J - V_{N_2}}{R_V} + \frac{V_J - V_{N_4}}{R_V} = 0$ Since $R_V$ is finite and non-zero, we can multiply by $R_V$: $(V_J - V_{N_1}) + (V_J - V_{N_2}) + (V_J - V_{N_4}) = 0$ $3V_J - (V_{N_1} + V_{N_2} + V_{N_4}) = 0$ $V_J = \frac{V_{N_1} + V_{N_2} + V_{N_4}}{3}$ Substitute the potentials: $V_J = \frac{2V_0/3 + V_0/3 + V_0/3}{3} = \frac{4V_0/3}{3} = \frac{4V_0}{9}$.

The reading of voltmeter $V_1$ is the magnitude of the potential difference between $N_1$ and J: Reading of $V_1 = |V_{N_1} - V_J| = |2V_0/3 - 4V_0/9|$ To subtract, find a common denominator (9): Reading of $V_1 = |\frac{6V_0}{9} - \frac{4V_0}{9}| = |\frac{2V_0}{9}| = \frac{2V_0}{9}$.

The final answer is \boxed{\text{a) V_0/6, b) 2V_0/9}}.

Solution: (a) When switch 'S' is open: The left branch is a voltage divider with potentials $V_{N_1} = 2V_0/3$ and $V_{N_2} = V_0/3$. The common junction J is connected to $N_1$ via $V_1$ and to $N_2$ via $V_2$. Since $V_1$ and $V_2$ are identical ideal voltmeters, they act as a voltage divider between $N_1$ and $N_2$. The potential at J is $V_J = (V_{N_1} + V_{N_2})/2 = (2V_0/3 + V_0/3)/2 = (V_0)/2$. The reading of $V_1 = |V_{N_1} - V_J| = |2V_0/3 - V_0/2| = |4V_0/6 - 3V_0/6| = V_0/6$.

(b) When switch 'S' is closed: The potentials $V_{N_1} = 2V_0/3$, $V_{N_2} = V_0/3$, and $V_{N_4} = V_0/3$. The common junction J is connected to $N_1$ via $V_1$, to $N_2$ via $V_2$, and to $N_4$ via $V_3$. Since all three voltmeters are identical and ideal, the potential at J is the average of the potentials they are connected to: $V_J = (V_{N_1} + V_{N_2} + V_{N_4})/3 = (2V_0/3 + V_0/3 + V_0/3)/3 = (4V_0/3)/3 = 4V_0/9$. The reading of $V_1 = |V_{N_1} - V_J| = |2V_0/3 - 4V_0/9| = |6V_0/9 - 4V_0/9| = 2V_0/9$.

Answer: (a) The reading of the voltmeter $V_1$ when switch 'S' is open is $V_0/6$. (b) The reading of the voltmeter $V_1$ after the switch is closed is $2V_0/9$.