Question

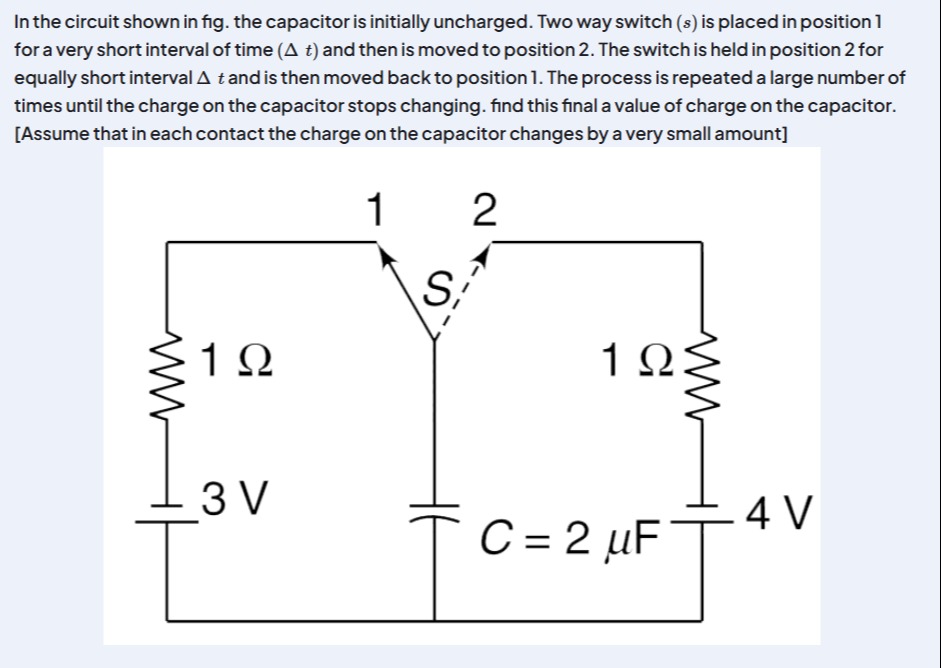
In the circuit shown in fig. the capacitor is initially uncharged. Two way switch (s) is placed in position 1 for a very short interval of time ($\Delta$ t) and then is moved to position 2. The switch is held in position 2 for equally short interval $\Delta$ t and is then moved back to position 1. The process is repeated a large number of times until the charge on the capacitor stops changing. find this final a value of charge on the capacitor. [Assume that in each contact the charge on the capacitor changes by a very small amount]

Answer 1

7 \mu C

Answer 2

The problem describes a circuit where a capacitor is repeatedly connected to two different voltage sources through resistors for very short intervals. The process continues until the charge on the capacitor reaches a steady state, meaning it no longer changes over a complete cycle of switching.

Let $Q$ be the charge on the capacitor at any given time, and $C$ its capacitance. The voltage across the capacitor is $V_C = Q/C$.

Step 1: Analyze the circuit when the switch S is in position 1. When the switch is in position 1, the capacitor is connected to the 3V battery and the 1Ω resistor on the left. The current $I_1$ flowing into the capacitor is given by Ohm's law: $I_1 = \frac{V_1 - V_C}{R_1} = \frac{3 \text{ V} - Q/C}{1 \text{ Ω}}$ Since the switch is held for a very short interval $\Delta t$, the change in charge on the capacitor, $\Delta Q_1$, can be approximated as: $\Delta Q_1 = I_1 \Delta t = \left(3 - \frac{Q}{C}\right) \Delta t$

Step 2: Analyze the circuit when the switch S is in position 2. When the switch is in position 2, the capacitor is connected to the 4V battery and the 1Ω resistor on the right. The current $I_2$ flowing into the capacitor is given by Ohm's law: $I_2 = \frac{V_2 - V_C}{R_2} = \frac{4 \text{ V} - Q/C}{1 \text{ Ω}}$ Since the switch is held for a very short interval $\Delta t$, the change in charge on the capacitor, $\Delta Q_2$, can be approximated as: $\Delta Q_2 = I_2 \Delta t = \left(4 - \frac{Q}{C}\right) \Delta t$

Step 3: Determine the final charge on the capacitor. The process is repeated until the charge on the capacitor stops changing. This means that in the final steady state, the net change in charge over one complete cycle (position 1 for $\Delta t$ then position 2 for $\Delta t$) is zero. Let $Q_f$ be this final charge. So, $\Delta Q_1 + \Delta Q_2 = 0$. Substituting the expressions for $\Delta Q_1$ and $\Delta Q_2$ with $Q = Q_f$: $\left(3 - \frac{Q_f}{C}\right) \Delta t + \left(4 - \frac{Q_f}{C}\right) \Delta t = 0$ Since $\Delta t$ is a non-zero interval, we can divide the equation by $\Delta t$: $3 - \frac{Q_f}{C} + 4 - \frac{Q_f}{C} = 0$ $7 - 2\frac{Q_f}{C} = 0$ $2\frac{Q_f}{C} = 7$ $Q_f = \frac{7C}{2}$

Step 4: Substitute the given values. The capacitance $C = 2 \mu\text{F} = 2 \times 10^{-6} \text{ F}$. $Q_f = \frac{7 \times (2 \times 10^{-6} \text{ F})}{2}$ $Q_f = 7 \times 10^{-6} \text{ C}$ $Q_f = 7 \mu\text{C}$

The final value of charge on the capacitor is $7 \mu\text{C}$.

The final answer is $\boxed{\text{7 \mu C}}$.

Explanation of the solution: The problem describes a switched-capacitor circuit reaching a steady state. In this state, the net change in charge on the capacitor over one complete switching cycle is zero.

1. When the switch is in position 1, the current is $I_1 = (3 - Q/C)/1$. The charge change is $\Delta Q_1 = I_1 \Delta t$.
2. When the switch is in position 2, the current is $I_2 = (4 - Q/C)/1$. The charge change is $\Delta Q_2 = I_2 \Delta t$.
3. For the charge to stop changing, the total charge change over one cycle must be zero: $\Delta Q_1 + \Delta Q_2 = 0$.
4. This leads to $(3 - Q_f/C)\Delta t + (4 - Q_f/C)\Delta t = 0$, which simplifies to $7 - 2Q_f/C = 0$.
5. Solving for $Q_f$, we get $Q_f = 7C/2$.
6. Substituting $C = 2 \mu\text{F}$, we find $Q_f = 7 \mu\text{C}$.

Answer: The final value of charge on the capacitor is $7 \mu\text{C}$.