Question

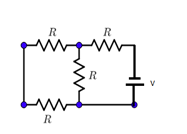
In the circuit shown. If the current in vertical resistance is equal to one. Then what is the potential of the battery?

$\left( A \right)\dfrac{{IR}}{2}$
$\left( B \right)\dfrac{{3IR}}{2}$
$\left( C \right)2IR$
$\left( D \right)\dfrac{{5IR}}{2}$

Answer 1

Apply Kirchhoff's law to find the potential of the battery. First Kirchhoff’s law on the loop ABCDA, then apply Kirchhoff's law on the loop ABCDA. Now you will end up with two equations. Subtract the two equations and apply the result in any one the two equations to obtain the potential of the battery.

Complete step by step answer:
Kirchhoff’s first law (junction law or current law): At any junction, the current leaving the junction is equal to current entering the system. Kirchhoff’s first law tells us that when steady current flows in the circuit then there will be no accumulation of charge at any point.
Kirchhoff’s second law (loop law or voltage law): The algebraic sum of changes in potential around any closed loop is zero.
Sign conventions:
-The change in potential passing through a resistance in the direction of current is $- IR$ while in the opposite direction $+ IR$.
-The change in potential passing through a emf source from positive to negative is $- E$ while in opposite direction $+ E$
Applying Kirchhoff’s law on the loop ABCDA we get
$IR + \left( {I + {I^1}} \right)R = e....\left( 1 \right)$
Where $I$is the main current flowing in the circuit and ${I^1}$ is the branch current in the circuit, e is the emf of the circuit.
Applying Kirchhoff’s law on the loop ABCDA we get
${I^1}\left( {R + R} \right) + \left( {I + {I^1}} \right)R = e....\left( 2 \right)$
Where $I$ is the main current flowing in the circuit and ${I^1}$ is the branch current in the circuit, e is the emf of the circuit
Subtract $eq\left( 2 \right) - eq\left( 1 \right)$ we get
$IR = 2R{I^1}$ OR
${I^1} = \dfrac{I}{2}$
Now substitute the value of ${I^1}$ in $eq\left( 1 \right)$
$e = IR + \left( {\dfrac{I}{2} + I} \right)R$
$e = IR + \dfrac{{3IR}}{2}$
$e = \dfrac{{5IR}}{2}$

So, the correct option is $\left( D \right)$

Note: According to the Kirchhoff’s first law of conservation of charge, since no charge can accumulate at a junction. Second law Kirchhoff’s law represents conservation of energy. Electric energy given to the charge by a source of emf is lost in passing through the resistance.