Question

In the circuit shown here, $E_1$ = $E_2$ = $E_3$ = $2$ $V$ and $R_1$ = $R_2$ = 4 ohms. What is the current flowing between points A and B through battery $E_2$?

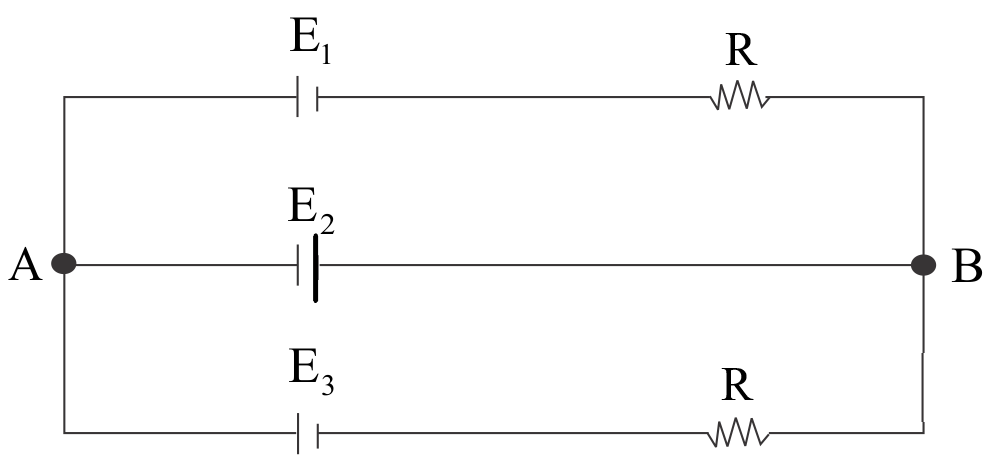
A) Zero
B) 2 amp from A to B
C) 2 amp from B to A
D) None of the above

Answer 1

Current flows through the path of least resistance. In the given circuit, find the equivalent emf and resistance. This can then be used to find the current flowing through the circuit.

Complete step by step solution:
We first need to simplify the circuit given to us. Since we need to find out the current through the battery $E_2$, we exclude it while finding out the equivalent emf of the batteries and the equivalent resistance. We only find the equivalent of $E_1$ and $E_3$ and the resistances $R_1$ and $R_2$.
The equivalent emf is given by the equation,
${E_{eq}} = \dfrac{{{E_1}{R_2} + {E_3}{R_1}}}{{{R_1} + {R_2}}} = \dfrac{{2 \times 4 + 2 \times 4}}{{4 + 4}} = \dfrac{{16}}{8} = 2$ V …equation (1)
We now find out the equivalent resistance in the circuit. Since the resistances are connected in parallel, we use the following equation to find the equivalent resistance,
${R_{eq}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{4 \times 4}}{{4 + 4}} = \dfrac{{16}}{8} = 2$ ohms

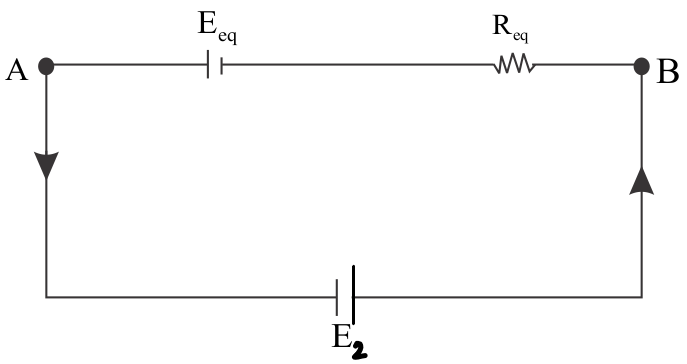
The current flowing through the circuit can be found out by dividing the potential difference between A and B by the equivalent resistance between the two points. We obtain,
$I = \dfrac{{{E_{eq}} + {E_2}}}{{{R_{eq}}}} = \dfrac{{2 + 2}}{2} = 2$ amps
We know that current flows from higher potential to lower potential. From the diagram, we can see that the current will flow in the anticlockwise direction as A is at higher potential than B. Current flows through the path with least resistance and the path with battery $E_2$ has no resistance. Therefore, 2 amps current flows from A to B through battery $E_2$.

Hence, the correct option is option B.

Note: If three cells, $E_1$, $E_2$ and $E_3$ are connected in parallel with internal resistances $R_1$, $R_2$, and $R_3$, then the equivalent emf and internal resistance are:
${R_{eq}} = \dfrac{{{r_1}{r_2}{r_3}}}{{{r_1}{r_2} + {r_2}{r_3} + {r_3}{r_1}}}$
${E_{eq}} = \dfrac{{\dfrac{{{E_1}}}{{{r_1}}} + \dfrac{{{E_2}}}{{{r_2}}} + \dfrac{{{E_3}}}{{{r_3}}}}}{{\dfrac{1}{{{r_1}}} + \dfrac{1}{{{r_2}}} + \dfrac{1}{{{r_3}}}}} = {R_{eq}}\left( {\dfrac{{{E_1}}}{{{r_1}}} + \dfrac{{{E_2}}}{{{r_2}}} + \dfrac{{{E_3}}}{{{r_3}}}} \right)$