Question

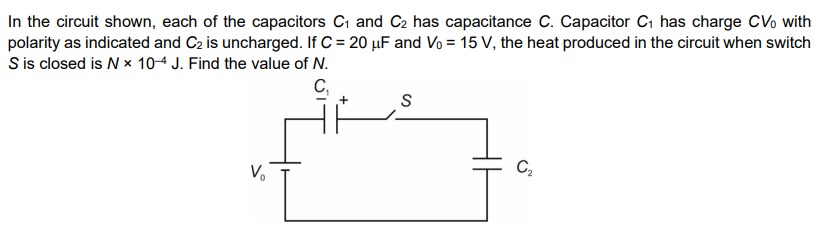
In the circuit shown, each of the capacitors C₁ and C₂ has capacitance C. Capacitor C₁ has charge CV₀ with polarity as indicated and C₂ is uncharged. If C = 20 µF and V₀ = 15 V, the heat produced in the circuit when switch S is closed is N x 10⁻⁴ J. Find the value of N.

Answer 1

22.5

Answer 2

The circuit consists of a voltage source $V_0$, a capacitor $C_1$ with capacitance $C$ and initial charge $Q_{1,initial} = CV_0$ with polarity as indicated (positive plate connected to the positive terminal of $V_0$), and a capacitor $C_2$ with capacitance $C$ and initial charge $Q_{2,initial} = 0$. When the switch S is closed, the capacitors $C_1$ and $C_2$ are connected in parallel with the voltage source $V_0$.

Initial state before closing the switch: The initial energy stored in capacitor $C_1$ is $U_{1,initial} = \frac{1}{2} \frac{Q_{1,initial}^2}{C_1} = \frac{1}{2} \frac{(CV_0)^2}{C} = \frac{1}{2} C V_0^2$. The initial energy stored in capacitor $C_2$ is $U_{2,initial} = \frac{1}{2} \frac{Q_{2,initial}^2}{C_2} = \frac{1}{2} \frac{0^2}{C} = 0$. The total initial energy stored in the capacitors is $U_{initial} = U_{1,initial} + U_{2,initial} = \frac{1}{2} C V_0^2$.

Final state after closing the switch and reaching equilibrium: In the final state, both capacitors are connected in parallel to the voltage source $V_0$. Thus, the potential difference across each capacitor is $V_0$. The final charge on capacitor $C_1$ is $Q_{1,final} = C_1 V_0 = CV_0$. The final charge on capacitor $C_2$ is $Q_{2,final} = C_2 V_0 = CV_0$. The final energy stored in capacitor $C_1$ is $U_{1,final} = \frac{1}{2} C_1 V_0^2 = \frac{1}{2} C V_0^2$. The final energy stored in capacitor $C_2$ is $U_{2,final} = \frac{1}{2} C_2 V_0^2 = \frac{1}{2} C V_0^2$. The total final energy stored in the capacitors is $U_{final} = U_{1,final} + U_{2,final} = \frac{1}{2} C V_0^2 + \frac{1}{2} C V_0^2 = C V_0^2$.

To find the heat produced, we can use the energy conservation principle. The work done by the voltage source is equal to the increase in the stored energy of the capacitors plus the heat dissipated in the circuit. $W_{source} = \Delta U_{capacitors} + Q_{heat}$ $\Delta U_{capacitors} = U_{final} - U_{initial} = C V_0^2 - \frac{1}{2} C V_0^2 = \frac{1}{2} C V_0^2$.

Now we need to calculate the work done by the source. The work done by the source is $W_{source} = V_0 \times (\text{total charge flown from the source})$. Let's consider the charge flow from the positive terminal of the source. The positive terminal is connected to the positive plates of $C_1$ and $C_2$. Initial charge on the positive plate of $C_1$ is $+CV_0$. Initial charge on the positive plate of $C_2$ is $0$. Final charge on the positive plate of $C_1$ is $+CV_0$. Final charge on the positive plate of $C_2$ is $+CV_0$. The total initial charge on the plates connected to the positive terminal is $CV_0 + 0 = CV_0$. The total final charge on the plates connected to the positive terminal is $CV_0 + CV_0 = 2CV_0$. The charge flown from the positive terminal of the source is the increase in the total charge on these plates, which is $(2CV_0) - (CV_0) = CV_0$. The work done by the source is $W_{source} = V_0 \times (CV_0) = CV_0^2$.

Now, we can find the heat produced: $Q_{heat} = W_{source} - \Delta U_{capacitors} = CV_0^2 - \frac{1}{2} C V_0^2 = \frac{1}{2} C V_0^2$.

Given values are $C = 20 \, \mu F = 20 \times 10^{-6} \, F$ and $V_0 = 15 \, V$. $Q_{heat} = \frac{1}{2} \times (20 \times 10^{-6} \, F) \times (15 \, V)^2$ $Q_{heat} = \frac{1}{2} \times 20 \times 10^{-6} \times 225 \, J$ $Q_{heat} = 10 \times 10^{-6} \times 225 \, J$ $Q_{heat} = 2250 \times 10^{-6} \, J$ $Q_{heat} = 2.25 \times 10^{-3} \, J$.

The heat produced is given as $N \times 10^{-4} \, J$. So, $N \times 10^{-4} = 2.25 \times 10^{-3}$ $N \times 10^{-4} = 22.5 \times 10^{-4}$ $N = 22.5$.

The final answer is $\boxed{22.5}$.

Explanation of the solution: Initial energy stored in $C_1$ is $U_{1,initial} = \frac{1}{2} C V_0^2$. Initial energy in $C_2$ is $U_{2,initial} = 0$. Total initial energy $U_{initial} = \frac{1}{2} C V_0^2$. When the switch is closed, $C_1$ and $C_2$ are in parallel with $V_0$. Final voltage across both is $V_0$. Final energy in $C_1$ is $U_{1,final} = \frac{1}{2} C V_0^2$. Final energy in $C_2$ is $U_{2,final} = \frac{1}{2} C V_0^2$. Total final energy $U_{final} = C V_0^2$. Change in stored energy $\Delta U = U_{final} - U_{initial} = C V_0^2 - \frac{1}{2} C V_0^2 = \frac{1}{2} C V_0^2$. Initial charge on positive plates connected to source is $CV_0$ (from $C_1$) + 0 (from $C_2$) = $CV_0$. Final charge on positive plates connected to source is $CV_0$ (on $C_1$) + $CV_0$ (on $C_2$) = $2CV_0$. Charge flown from source $\Delta Q_{source} = 2CV_0 - CV_0 = CV_0$. Work done by source $W_{source} = V_0 \times \Delta Q_{source} = V_0 \times CV_0 = CV_0^2$. Heat produced $Q_{heat} = W_{source} - \Delta U = CV_0^2 - \frac{1}{2} C V_0^2 = \frac{1}{2} C V_0^2$. Substitute $C = 20 \times 10^{-6} \, F$ and $V_0 = 15 \, V$. $Q_{heat} = \frac{1}{2} \times (20 \times 10^{-6}) \times (15)^2 = 10 \times 10^{-6} \times 225 = 2250 \times 10^{-6} = 2.25 \times 10^{-3} \, J$. Given $Q_{heat} = N \times 10^{-4} \, J$. $N \times 10^{-4} = 2.25 \times 10^{-3} = 22.5 \times 10^{-4}$. $N = 22.5$.