Question
Question: In the circuit shown current through inductor L as a function of time t is (if switch is closed at t...
In the circuit shown current through inductor L as a function of time t is (if switch is closed at t = 0)
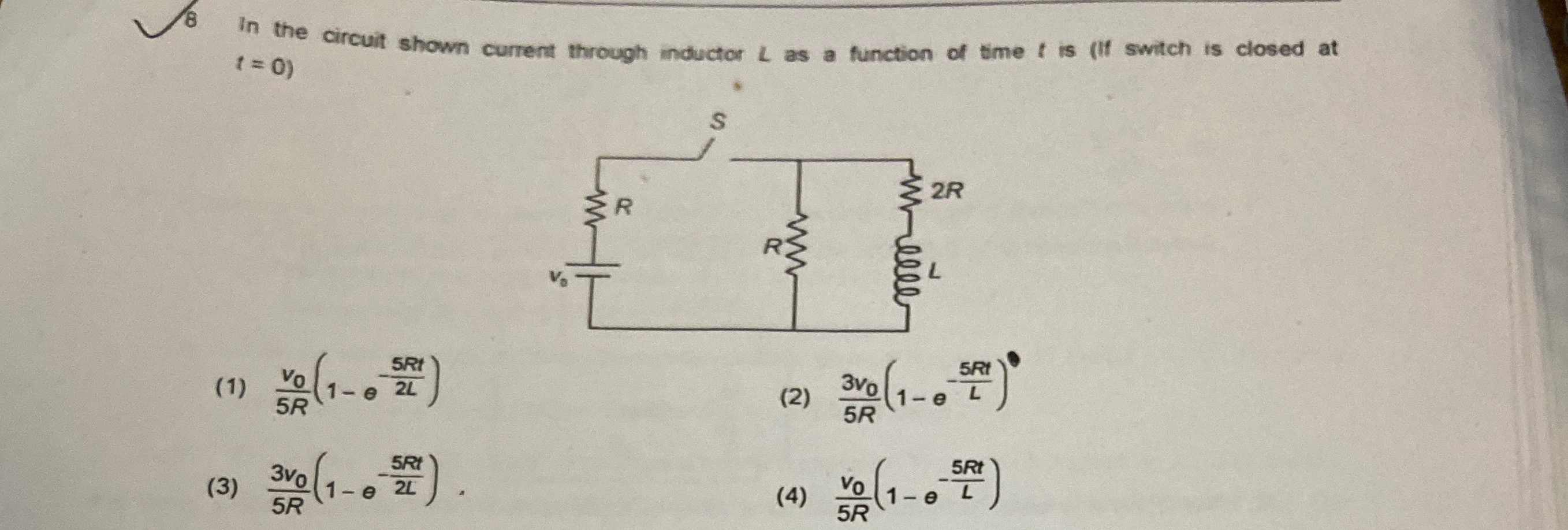
5RV0(1−e2L−5Rt)
5R3V0(1−eL−5Rt)
5R3V0(1−e2L−5Rt)
5RV0(1−eL−5Rt)
(1) 5RV0(1−e2L−5Rt)
Solution
To determine the current through the inductor L as a function of time t, we need to find the steady-state current (I0) through the inductor and the time constant (τ) of the RL circuit. The general form for current growth in an RL circuit is I(t)=I0(1−e−t/τ).
1. Calculate the steady-state current (I0) through the inductor:
At steady state (t → ∞), an inductor acts as a short circuit (its resistance becomes zero). The circuit simplifies as follows:
- The resistor R (in series with V0) is in series with the parallel combination of the other resistor R and the 2R resistor (which is in series with the shorted inductor).
- The equivalent resistance of the parallel combination of R and 2R is: Rparallel=R+2RR×2R=3R2R2=32R
- The total equivalent resistance of the circuit at steady state is: Rtotal=R+Rparallel=R+32R=35R
- The total current drawn from the source is: Isource=RtotalV0=5R/3V0=5R3V0
- This source current Isource splits between the parallel R and 2R branches. The current through the inductor branch (containing 2R) is I0. Using the current divider rule: I0=Isource×Rother_branch+Rinductor_branchRother_branch I0=5R3V0×R+2RR=5R3V0×3RR=31×5R3V0=5RV0
2. Calculate the Thevenin equivalent resistance (Rth) seen by the inductor:
To find Rth, we deactivate the independent voltage source (replace it with a short circuit) and look into the terminals where the inductor is connected.
- When the voltage source V0 is shorted, the resistor R (originally in series with V0) becomes parallel to the other resistor R.
- The equivalent resistance of this parallel combination is: Rparallel′=R+RR×R=2RR2=2R
- This Rparallel′ is in series with the 2R resistor (which is directly connected to the inductor terminals).
- Therefore, the Thevenin equivalent resistance seen by the inductor is: Rth=Rparallel′+2R=2R+2R=25R
3. Calculate the time constant (τ):
The time constant for an RL circuit is given by τ=RthL.
τ=5R/2L=5R2L
4. Formulate the current as a function of time:
Using the general formula I(t)=I0(1−e−t/τ):
I(t)=5RV0(1−e−t/(5R2L))
I(t)=5RV0(1−e−2L5Rt)
Comparing this result with the given options, it matches option (1).
