Question

In the circuit shown, current (in A) through the 50V and 30V batteries are, respectively :

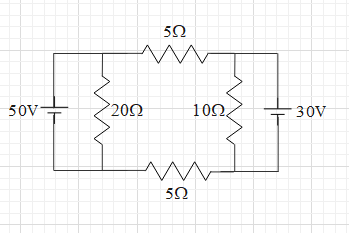
A. 3.5 and 2
B. 3 and 2.5
C. 2.5 and 3
D. 4.5 and 1

Answer 1

Find the currents through the resistances of 20$\Omega$ and 10$\Omega$ by using Ohm’s law. Then use junction law at points C and A and find the currents through both the 5$\Omega$ resistances in terms of current through battery 50V. Then find the value of the current through battery 50V by applying KVL for the outer loop. Use junction law at point D and then find the relation between the currents through both the batteries. Then find the value of the current in the other battery.

Formula used:
V=iR

Complete answer:
Let us first show the current in all the branches of the given circuit. Let the currents through the batteries of 50 V and 30 V be ${{i}_{1}}$ and ${{i}_{2}}$ respectively and shown in the figure below.

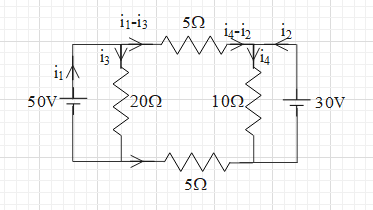
Let the currents through the resistances of 20$\Omega$ and 10$\Omega$ be ${{i}_{3}}$ and ${{i}_{4}}$ respectively.
The potential difference across the 20$\Omega$ resistance is 50V. Therefore, by applying Ohm’s law we get that $50=20{{i}_{3}}$.
$\Rightarrow {{i}_{3}}=\dfrac{20}{50}=2.5A$.
The potential difference across the 10$\Omega$ resistance is 30V. With the same law we get that $30=10{{i}_{4}}$
$\Rightarrow {{i}_{4}}=\dfrac{30}{10}=3A$.
From the junction law at point C, we get the current through the upsides resistance of 5$\Omega$ is ${{i}_{1}}-{{i}_{3}}={{i}_{1}}-2.5$.
Therefore, the potential difference across this resistance is $5\left( {{i}_{1}}-2.5 \right)$.
From the same law at point H, the current through the resistance of 5$\Omega$ down is ${{i}_{3}}-{{i}_{1}}=2.5-{{i}_{1}}$.
Therefore, the potential difference across this resistance is $5\left( 2.5-{{i}_{1}} \right)$.
Now, let us apply Kirchhoff’s loop law for the outer loop ABEFA.
Hence, we get
$50-5\left( {{i}_{1}}-2.5 \right)-30+5\left( 2.5-{{i}_{1}} \right)=0$
$\Rightarrow 20-5{{i}_{1}}+2.5(5)+2.5(5)-5{{i}_{1}}=0$
$\Rightarrow 20-10{{i}_{1}}+25=0$
$\Rightarrow {{i}_{1}}=\dfrac{45}{10}=4.5A$.
Therefore, the current through the battery of 50V is 4.5A.
Similarly, from the junction law at point D, we get the current through the upsides resistance of 5$\Omega$ is ${{i}_{3}}-{{i}_{2}}=3-{{i}_{2}}$.
But we already found the current equal to ${{i}_{1}}-2.5$.
This means that ${{i}_{1}}-2.5=3-{{i}_{2}}$
$\Rightarrow {{i}_{2}}=5.5-{{i}_{1}}$
Substitute the value of ${{i}_{1}}$.
$\Rightarrow {{i}_{2}}=5.5-4.5=1A$.
Therefore, the current through the battery of 30V is 1A.

Hence, the correct option is D.

Note: We can also find ${{i}_{2}}$ by applying junction law points D and G and writing the current in both the resistance of 5$\Omega$ in terms of ${{i}_{2}}$. Then apply Kirchhoff’s loop law for the same loop ABEFA. With this we will find the value of ${{i}_{2}}$.