Question

In the circuit shown below, the reading of the voltmeter V is
A.12V
B.8V
C.20V
D.16V

Answer 1

As we can see, the two resistors which are connected to the voltmeter are connected in parallel. So, first find the potential difference along the path where the $4\Omega$ resistor is connected. Then, find the potential difference along the path where the $16\Omega$ resistor is connected. Subtract these two potential differences and find the reading on the voltmeter V. To find the potential across the resistor use Ohm’s law.

Complete answer:

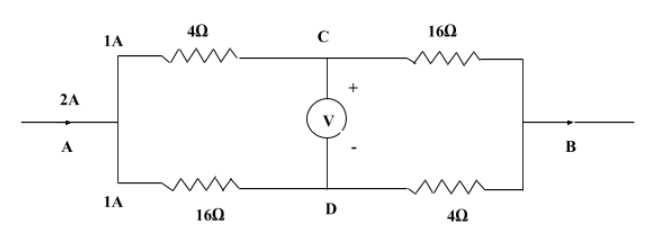
Let the potential at point A be ${V}_{A}$
Potential difference across points A and C is given by,
${V}_{AC} ={V}_{A}-{V}_{C}$ …(1)
From Ohm’s law we know,
$V=IR$
Therefore, potential across $4\Omega$ resistance is.
${V}_{C} = 1 \times 4$
$\Rightarrow{V}_{C} = 4V$
Substituting this value in the equation. (1) we get,
${V}_{AC} ={V}_{A}-4$ …(2)
Similarly, potential difference across points A and D is given by,
${V}_{AD} ={V}_{A}-{V}_{D}$ …(3)
Potential across $16\Omega$ resistance is.
${V}_{D} = 1 \times 16$
$\Rightarrow{V}_{C} = 16V$
Substituting this value in the equation. (1) we get,
${V}_{AD} ={V}_{A}-16$ …(4)
Thus, potential difference across points C and D is given by,
${V}_{CD} ={V}_{AC}-{V}_{AD}$
Substituting equation. (2) and (4) in above equation we get,
${V}_{CD}= {V}_{A}-4 - {V}_{A}+16$
$\Rightarrow {V}_{CD}= 16-4$
$\Rightarrow {V}_{CD}= 12V$
Hence, the reading of the voltmeter V is 12V.

So, the correct answer is option A i.e. 12V.

Note:
When the resistors are connected in series, there is only one path for the current to flow. Thus, equal current flows through each resistor. But, the potential drop across all the resistors in series may not be the same.
When the resistors are connected in parallel, there are many paths for the current to flow. The current may not be the same through each path in the circuit. But, the potential drop across all the resistors connected in parallel is the same.