Question
Question: In the circuit shown below current \({{I}_{0}}\) flowing through \(6\Omega \) resistance and voltage...
In the circuit shown below current I0 flowing through 6Ω resistance and voltage drop V0 across 3Ω resistance respectively are-
(A). 32A,4V
(B). 32A,2V
(C). 31A,2V
(D). 31A,4V
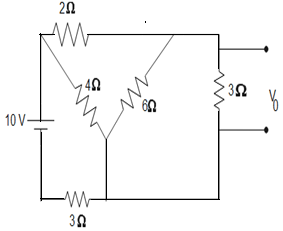
Solution
The figure shown above contains resistors connected in series and parallel. By resolving the circuit, we can calculate the total resistance in the circuit. Using the ohm’s law, we can calculate the current and potential drop for individual resistances and hence find the result.
Formulas used:
R=IV
Complete answer:
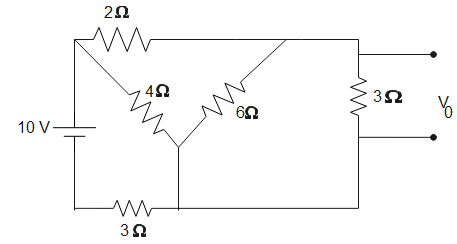
In the given circuit, 6Ω and 3Ω are in parallel so their equivalent resistance will be-
R=6+36×3⇒R=2Ω
The equivalent resistance is 2Ω. The figure can be simplified as-
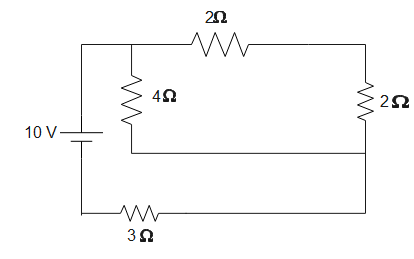
In the above figure 2Ω and 2Ω are in series, therefore, the equivalent resistance will be-
R′=2+2=4Ω
Therefore, the equivalent resistance is 4Ω. The above figure can be simplified as
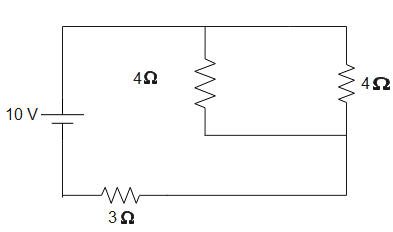
In the above figure, 4Ω and 4Ω are in parallel. Therefore, their equivalent resistance will be-
R′′=4+44×4⇒R′′=2Ω
The equivalent resistance is 2Ω and this equivalent resistance is in series with 3Ω aso the equivalent resistance is-
R′′′=2+3=5Ω
The total resistance in the circuit is 5Ω.
According to Ohm’s law,
R=IV - (1)
Here, V is the potential difference
R is the resistance
I is the current
Given, R=5Ω, V=10V. We substitute given values in the above equation to get,
10=I5⇒I=510∴I=2A
Therefore, the total current in the circuit is 2A.
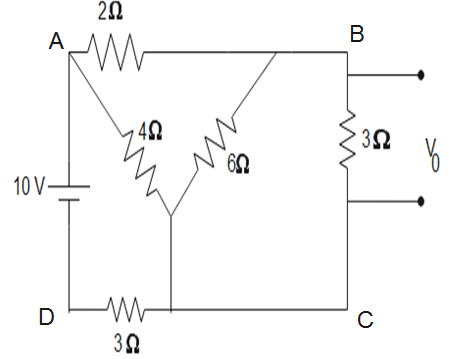
The circuit given above can be simplified as-
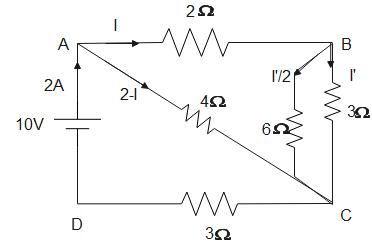
Applying loop in DACD, we get,
10−4(2−I)−3(2)=0⇒10−8+4I−6=0⇒I=1A
Therefore, I=1A
Applying both loops of ABCDA,
10−2(1)−3I′−3(2)=0⇒I′=32A
Therefore, I′=32A, so 2I′=21×32=31A
Therefore, the value of I0=31A.
The potential difference across 3Ω between BC is V0. From eq (1), the value of V0 is-
V0=32×3⇒V0=2V
Therefore, the value of V0 and I0 respectively are 2V,31A.
Hence, the correct option is (C).
Note:
The Kirchhoff’s voltage law states that the sum of all potential differences in a loop is zero. It follows the law of conservation of energy. The potential in a wire is the same everywhere unless an element is introduced in it. The series current through the resistors is the same while in parallel, the potential drop on resistors is the same.
