Question

In the circuit shown, A and B are equal resistances. When S is closed, the capacitor C charges from the cell of emf $\varepsilon$ and reaches a steady state.

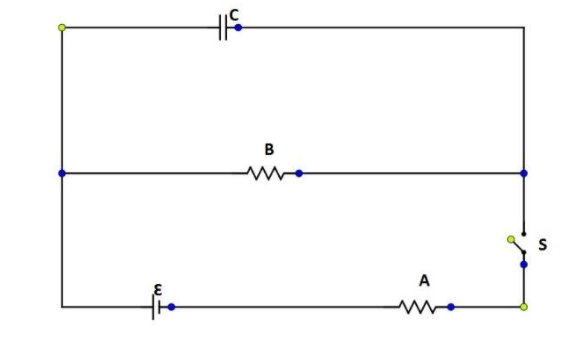
(A) During charging, more heat is produced in A than in B.
(B) In the steady state, heat is produced at the same rate in A and B.
(C) In the steady state, energy stored in $C$ is$\dfrac{1}{4}C{\varepsilon ^2}$.
(D) In the steady state, energy stored in $C$ is$\dfrac{1}{2}C{\varepsilon ^2}$.

Answer 1

The current through A is the main current passing through the battery. Heat is dependent on the square of current, the resistance and time. Energy stored in a capacitor is electrical potential energy.

Formula used: The formulae used in the solution are given here.
$H = {I^2}RT$ where $H$ is the heat produced when a current of $I$ amperes passes through a circuit of resistance $R$ ohms for a time of $t$ seconds.
Charge $Q$ and voltage $V$ are related to the capacitance $C$ of a capacitor by $Q = CV$.
${U_{Cap}} = \dfrac{{QV}}{2} = \dfrac{{C{V^2}}}{2}$ where ${U_{Cap}}$ is the energy stored in a capacitor, charge is $Q$ and voltage is $V$.

Complete step by step answer: Given in question, A and B are equal resistances. A and B resistors are connected in a parallel circuit. Capacitor C is connected in parallel with this circuit. When S is closed, the capacitor C charges from the cell of emf $\varepsilon$ and reaches a steady state.
Let the current passing through resistor A be ${I_A}$, that passing through resistor B be ${I_B}$ and the current passing through capacitor C be ${I_C}$.
During charging the current through A is the main current passing through the battery. So, this current is more than the current passing through B, i.e., $I = {I_A}$. This current is equivalent to the sum of currents passing through B and C.
Thus, ${I_A} = {I_B} + {I_C}$.
We know that, $H = {I^2}RT$. Thus, when a current of $I$ amperes passes through a circuit of resistance $R$ ohms for a time of $t$ seconds then the heat produced is given by the relation. It is thus evident that, during charging more heat is produced in A.
In steady state, no current flow in the capacitor wire so ${I_C} = 0$.
So, ${I_A} = {I_B}$.
Hence heat is produced at the same rate in both the resistors A and B.
Energy stored in a capacitor is electrical potential energy, and it is thus related to the charge and voltage on the capacitor.
Charge $Q$ and voltage $V$ are related to the capacitance $C$ of a capacitor by $Q = CV$.
${U_{Cap}} = \dfrac{{QV}}{2} = \dfrac{{C{V^2}}}{2}$
In the circuit given, $\varepsilon$ is the electromotive force of the cell.
Thus, ${V_C} = {V_B} = \dfrac{\varepsilon }{2}$
$\therefore U = \dfrac{1}{2}C{V_C}^2 = \dfrac{1}{2}C{\varepsilon ^2}$.
Further, in the steady state, the energy stored in $C$ is $\dfrac{1}{2}C{\varepsilon ^2}$.

Hence the Options A, B and D are true for this circuit.

Note: A parallel circuit is defined as one where all components are connected between the same set of electrically common points. Another way of saying this is that all components are connected across each other’s terminals. From this definition, three rules of parallel circuits follow:
1. All components share the same voltage.
2. Resistances diminish to equal a smaller, total resistance.
3. Branch currents add to equal a larger, total current.
Just as in the case of series circuits, all of these rules find root in the definition of a parallel circuit.